Viết phương trình đường vuông góc chung của các cặp đường thẳng sau :
LG a
d:x−22=y−33=z+4−5,d′:x+13=y−4−2=z−4−1
Lời giải chi tiết:
Cách 1: Ta có →ud=(2;3;−5),→ud′=(3;−2;−1).
Khi đó vì [→ud,→ud′]=(−13;−13;−13) nên đường vuông góc chung Δ có một vectơ chỉ phương là →u=(1;1;1).
Gọi (α) là mặt phẳng chứa d và Δ thì (α) đi qua Mo(2;3;−4) và có vectơ pháp tuyến →nα=[→ud,→u]=(8,−7,−1).
Có phương trình của mp(α) là: 8(x−2)−7(y−3)−1(z+4)=0
⇔8x−7y−z+1=0.
Gọi (β) là mặt phẳng chứa d′ và Δ thì (β) đi qua điểm M′o(−1;4;4) và có vectơ pháp tuyến →nβ=[→u,→ud′]=(1;4;−5).
Phương trình của mp(β) là :1(x+1)+4(y−4)−5(z−4)=0
⇔x+4y−5z+5=0.
Vậy đường vuông góc chung Δ của d và d′ là giao tuyến của hai mặt phẳng (α) và (β) . Nó có phương trình tham số là:
{x=ty=tz=1+t.
Cách 2: Điểm M∈d có toa độ là M=(2+2t;3+3t;−4−5t).
Điểm N∈d′ có toa độ là N=(−1+3t′;4−2t′;4−t′)
⇒→MN=(−3+3t′−2t;1−2t′−3t;8−t′+5t).
MN là đường vuông góc chung của d và d′ khi và chỉ khi
{→MN.→ud=0→MN.→ud′=0
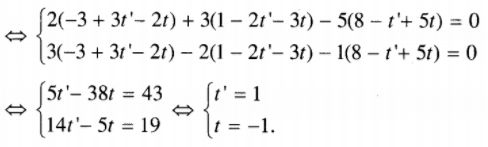
Suy ra M=(0;0;1),N=(2;2;3)⇒→MN=(2;2;2).
Vậy phương trình chính tắc của đường vuông góc chung Δ là
x1=y1=z−11.
LG b
d:{x=2+ty=1−tz=2t,d′:{x=2−2t′.y=3z=t′.
Lời giải chi tiết:
x−21=y−35=z2.

