LG a
Cho đường thẳng d là giao tuyến của hai mặt phẳng
\(\left( \alpha \right):x + y + z + 1 = 0\) và \(\left( {\alpha '} \right):x - y + z - 1 = 0;\)
Và cho hai mặt phẳng \(\eqalign{ & \left( {{P_1}} \right):x + 2y + 2z + 3 = 0 \cr & \left( {{P_2}} \right):x + 2y + 2z + 7 = 0 \cr} \)
Viết phương trình mặt cầu có tâm I thuộc d và tiếp xúc với cả hai mặt phẳng (P1) và (P2).
Lời giải chi tiết:
Ta nhận thấy mp(\({P_1}\)) song song với mp(\({P_2}\)).
Gọi A là giao điểm của đường thẳng d với mp(\({P_1}\)). Tọa độ (x; y; z) của A là nghiệm của hệ: \(\left\{ \matrix{ x + y + z + 1 = 0 \hfill \cr x - y + z - 1 = 0 \hfill \cr x + 2y + 2z + 3 = 0 \hfill \cr} \right.\)
Suy ra \(A = \left( {1; - 1; - 1} \right).\)
Gọi B là giao điểm của đường thẳng d với mp(\({P_2}\)). Toa độ (x; y; z) của B là nghiệm của hệ: \(\left\{ \matrix{ x + y + z + 1 = 0 \hfill \cr x - y + z - 1 = 0 \hfill \cr x + 2y + 2z + 7 = 0 \hfill \cr} \right.\)
Suy ra \(B = \left( {5; - 1; - 5} \right).\)
Tâm I của mặt cầu phải tìm là trung điểm của đoạn thẳng AB.
Do đó \(I = \left( {3; - 1; - 3} \right)\). Bán kính của mặt cầu phải tìm là
\(R = d\left( {I,\left( {{P_1}} \right)} \right) = {{\left| {3 - 2 - 6 + 3} \right|} \over {\sqrt 9 }} = {2 \over 3}.\)
Vậy phương trình mặt cầu cần tìm là:
\({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 3} \right)^2} = {4 \over 9}.\)
LG b
Cho đường thẳng \(d:{x \over 2} = {{y - 1} \over 1} = {{z + 1} \over 2}\) và hai mặt phẳng
\(\eqalign{
& \left( {{P_1}} \right):x + y - 2z + 5 = 0 \cr
& \left( {{P_2}} \right):2x - y + z + 2 = 0 \cr} \)
Lời giải chi tiết:
Gọi \(I = \left( {a;b;c} \right)\) là tâm mặt cầu cần tìm, do \(I \in d\) nên
\({a \over 2} = {{b - 1} \over 1} = {{c + 1} \over 2} \Leftrightarrow \left\{ \matrix{ a - 2b + 2 = 0 \hfill \cr a - c - 1 = 0. \hfill \cr} \right.\)
Vì mặt cầu (S) tiếp xúc với cả mp(\({P_1}\)) và mp(\({P_2}\)) nên:
\(d\left( {I,\left( {{P_1}} \right)} \right) = d\left( {I,\left( {{P_2}} \right)} \right) = R\)
\( \Leftrightarrow {{\left| {a + b - 2c + 5} \right|} \over {\sqrt 6 }} = {{\left| {2a - b + c + 2} \right|} \over {\sqrt 6 }} \Leftrightarrow \left[ \matrix{ a - 2b + 3c = 3 \hfill \cr 3a - c = - 7. \hfill \cr} \right.\)
Kết hợp với điều kiện trên ta có:
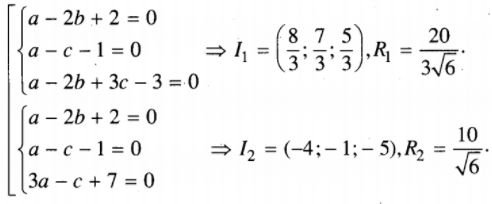
Vậy có 2 mặt cầu có tâm nằm trên \(d\) và tiếp xúc với \(\left( {{P_1}} \right),\left( {{P_2}} \right)\) , chúng có phương trình là
\(\eqalign{ & {\left( {x - {8 \over 3}} \right)^2} + {\left( {y - {7 \over 3}} \right)^2} + {\left( {z- {5 \over 3}} \right)^2} = {{200} \over {27}}; \cr & {\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 5} \right)^2} = {{50} \over 3}. \cr} \)

