LG a
Viết phương trình mặt cầu đi qua A(1;2;-4), B(1;-3;1), C(2;2;3) và có tâm nằm trên mp(Oxy).
Lời giải chi tiết:
Gọi I là tâm mặt cầu. Vì I∈mp(Oxy) nên I=(x;y;0). Theo giả thiết, ta có AI2=BI2=CI2, suy ra
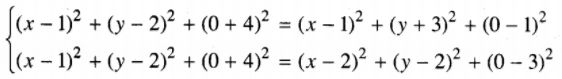
⇒{x=−2y=1⇒I(−2;1;0).
Bán kính của mặt cầu là:
R=AI=√(−2−1)2+(1−2)2+42=√26
Vậy phương trình mặt cầu là:
(x+2)2+(y−1)2+z2=26.
LG b
Viết phương trình mặt cầu đi qua hai điểm A(3;-1;2), B(1;1;-2) và có tâm thuộc trục Oz.
Lời giải chi tiết:
Gọi I là tâm mặt cầu, I∈Oz nên I = (0;0;z).
Theo giả thiết AI2=BI2, ta có phương trình
(−3)2+12+(z−2)2=(−1)2+(−1)2+(z+2)2
⇒8z=8⇒z=1
Vậy I=(0;0;1) và AI=√11.
Phương trình mặt cầu cần tìm là
x2+y2+(z−1)2=11
LG c
Viết phương trình mặt cầu đi qua bốn điểm A(1;1;1), B(1;2;1), C(1;1;2), D(2;2;1).
Lời giải chi tiết:
Phương trình mặt cầu (S) cần tìm có dạng
Ta có : (x)2+(y)2+(z)2−2ax−2by−2cz+d=0A∈(S)⇔2a+2b+2c−d=3.B∈(S)⇔2a+4b+2c−d=6.C∈(S)⇔2a+2b+4c−d=6.D∈(S)⇔4a+4b+2c−d=9.
Từ đó ta suy ra a=32;b=32;c=32;d=6.
Vậy phương trình mặt cầu là :
x2+y2+z2−3x−3y−3z+6=0.

