Cho tam giác AIB có IA = IB = 2a, ^AIB =1200. Trên đường thẳng Δ vuông góc với mp(AIB) tại I, lấy các điểm C và D sao cho ABC là tam giác vuông, ABD là tam giác đều.
LG 1
Tính thể tích và diện tích toàn phần cửa tứ diện ABCD.
Lời giải chi tiết:
Vì IA = IB = 2a, ^AIB =1200 nên AB2=IA2+IB2−2IA.IB.cos ^AIB =12a2, từ đó AB=2a√3. Do CD⊥mp(AIB) tại I, IA = IB nên CA = CB. Kết hợp với giả thiết ABC là tam giác vuông, ta có ABC là tam giác vuông tại C và CA=CB=AB√2=a√6.
Vì ABD là tam giác đều nên AD=AB=2a√3.
Từ đó CI2=AC2−AI2=6a2−4a2=2a2, tức là CI=a√2,
DI2=AD2−AI2=12a2−4a2=8a2, tức là DI=2a√2,
∙ Hai điểm C, D thuộc đường thẳng Δ vuông góc với mp(AIB) tại điểm I nên có hai trường hợp xảy ra.
+) Trường hợp 1. C, D nằm về hai phía đối với điểm I.
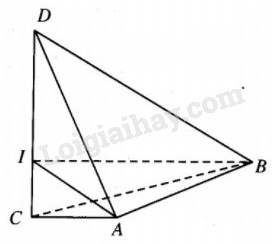
Dễ thấy CD=3a√2, từ đó CD2=18a2; mặt khác AC2+AD2=18a2, tức là CD2=AC2+AD2. Như vậy ^CAD = 900. Tương tự ta cũng có ^CBD = 900.
VABCD=VD.AIB+VC.AIB
=13.12AI.BIsin^AIB.(ID+IC)
=13.12.2a.2a.√32.3a√2=a3√6.
Gọi Stp là diện tích toàn phần của tứ diện ABCD thì
Stp=SACD+SBCD+SABC+SABD=2.12CD.AI+AC22+AB2√34=3a√2.2a+12.6a2+12a2.√34=6a2√2+3a2+3a2√3=3a2(1+√3+2√2)
+) Trường hợp 2. C, D nằm về một phía đổi với điểm I.
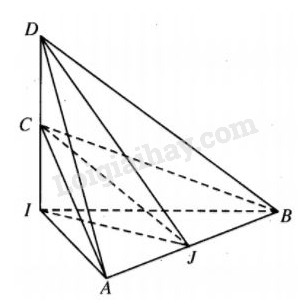
VABCD=VDAIB−VCAIB=a3√63,Stp=2a2√2+3a2+3a2√3=a2(3+2√2+3√3).
LG 2
Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD.
Lời giải chi tiết:
+) Trường hợp 1.
Vì ^CAD=^CBD = 900 nên CD là đường kính của mặt cầu ngoại tiếp tứ diện ABCD, từ đó bán kính mặt cầu phải tìm bằng 3a√22 và diện tích mặt cầu bằng 18πa2.
+) Trường hợp 2.
Gọi J là trung điểm của AB thì JA = JB = JC.
Xét đường thẳng Δ1 đi qua J và vuông góc với mp(ABC).
Khi đó, mọi điểm thuộc Δ1 cách đều các điểm A, B, C và Δ1 nằm trong mp(CDJ) ( do mp(CDJ) vuông góc với mp(ABC)).
Trong mp(CDJ), đường trung trực của CD cắt Δ1 tại điểm O thì OA = OB = OC = OD = R.
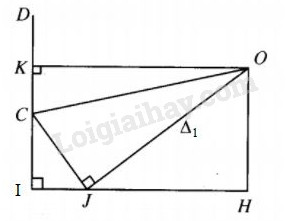
Ta có IJ=a,CJ=a√3. Kẻ OH⊥IJ thì
OH=IK=3a√22. Xét các tam giác ICJ và HJO, ta có sin C = sin J hay IJJC=OHJO. Vậy JO=OH.JCIJ=3a√22.a√3a=3a√62.
Từ đó OC2=CJ2+JO2=3a2+54a24=66a24.
Vậy diện tích mặt cầu phải tìm là 66πa2.
LG 3
Tính bán kính mặt cầu nội tiếp tứ diện ABCD.
Lời giải chi tiết:
+) Trường hợp 1.
Gọi r là bán kính mặt cầu nội tiếp tứ diện ABCD thì dễ thấy r=3VABCDStp, từ đó
r=3a3√63a2(1+√3+2√2)=a√61+√3+2√2.
+) Trường hợp 2.
r=a3√6a2(3+2√2+3√3)=a√63+3√3+2√2.

