Cho hình trụ có bán kính bằng R, trục OO’ bằng h. Một mặt phẳng (P) thay đổi đi qua O, tạo với đáy hình trụ góc α cho trước và cắt hai đáy của hình trụ đã cho theo các dây AB và CD ( dây AB đi qua O).
LG 1
Tính diện tích tứ giác ABCD.
Lời giải chi tiết:
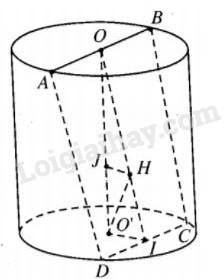
Gọi I là trung điểm của CD thì O′I⊥CD, từ đó OI⊥CD. Vậy α=^OIO′.
Dễ thấy AB//CD, tức là ABCD là hình thang. Mặt khác OI⊥CD nên OI⊥AB.
Vậy ABCD là hình thang cân.
Diện tích S của ABCD được tính bởi
S=12(AB+CD).OI
Ta có : AB=2R,OI=OO′sinα=hsinα.
O′I=OO′cotα⇒ID=√O′D2−O′I2=√R2−h2cot2α⇒CD=2√R2−h2cot2α.
Vậy S=12(2R+2√R2−h2cot2α).hsinα
=(R+√R2−h2cot2α).hsinα.
LG 2
Chứng minh rằng hình chiếu vuông góc H của điểm O’ trên (P) thuộc một đường tròn cố định.
Lời giải chi tiết:
Trong mặt phẳng (OO’I), kẻ O′H⊥OI thì H là hình chiếu của O’ trên mp(P).
Xét tam giác vuông O’IH, ta có O′H=O′Isinα=h.cotα.sinα=h.cosα.
Kẻ đường cao HJ của tam giác vuông O’HO thì O′J.OO′=O′H2,
⇒O′J=O′H2OO′=h.cos2α, từ đó suy ra J là điểm cố định.
Mặt khác HJ2=O′H2−O′J2
=h2.cos2α−h2.cos4α
=h2cos2α.sin2α.
Vậy HJ có độ dài không đổi, từ đó ta có điểm H thuộc đường tròn tâm J, bán kính cho trước, trong mặt phẳng vuông góc với OO’ tại J.
Chú ý. Cũng có thể thấy H thuộc mặt trụ T có trục là OO’, bán kính đáy R’ cho trước.
Cụ thể R′=h.cosα.sinα, đồng thời H thuộc mặt phẳng vuông góc với trục OO’ tại điểm J.
Từ đó H thuộc đường tròn là giao của mặt trụ T và mặt phẳng nói trên.

