Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau:
LG a
\(f(x) = {x^3} + 3{x^2} - 9x + 1\) trên đoạn [-4;4]
Lời giải chi tiết:
\(\begin{array}{l}
f'\left( x \right) = 3{x^2} + 6x - 9\\
f'\left( x \right) = 0 \Leftrightarrow 3{x^2} + 6x - 9 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 1 \in \left[ { - 4;4} \right]\\
x = - 3 \in \left[ { - 4;4} \right]
\end{array} \right.\\
f\left( { - 4} \right) = 21,f\left( 4 \right) = 77\\
f\left( 1 \right) = - 4,f\left( { - 3} \right) = 28
\end{array}\)
Vậy \(\mathop {\min }\limits_{x \in \left[ { - 4;4} \right]} f(x) = f(1) = - 4;\)
\(\mathop {{\rm{max}}}\limits_{x \in \left[ { - 4;4} \right]} {\rm{ }}f(x){\rm{ }} = f(4) = 77\)
LG b
\(f(x) = {x^3} + 5x - 4\) trên đoạn [-3;1]
Lời giải chi tiết:
\(f'\left( x \right) = 3{x^2} + 5 > 0,\forall x \in \mathbb{R}\)
Do đó hàm số đồng biến trên \(\mathbb{R}\) hay cũng đồng biến trên \(\left[ { - 3;1} \right]\).
\( \Rightarrow \)\(\mathop {\min }\limits_{x \in \left[ { - 3;1} \right]} f(x) = f( - 3) = - 46;\)
\(\mathop {\max }\limits_{x \in \left[ { - 3;1} \right]} f(x) = f(1) = 2\)
LG c
\(f(x) = {x^4} - 8{x^2} + 16\) trên đoạn [-1;3]
Lời giải chi tiết:
\(\begin{array}{l}
f'\left( x \right) = 4{x^3} - 16x\\
f'\left( x \right) = 0 \Leftrightarrow 4{x^3} - 16x = 0\\
\Leftrightarrow 2x\left( {{x^2} - 4} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 0 \in \left[ { - 1;3} \right]\\
x = 2 \in \left[ { - 1;3} \right]\\
x = - 2 \notin \left[ { - 1;3} \right]
\end{array} \right.\\
f\left( { - 1} \right) = 9,f\left( 3 \right) = 25\\
f\left( 0 \right) = 16,f\left( 2 \right) = 0
\end{array}\)
Vậy:
\(\mathop {\min }\limits_{x \in \left[ { - 1;3} \right]} f(x) = f(2) = 0\)
\(\mathop {\max }\limits_{x \in \left[ { - 1;3} \right]} f(x) = f(3) = 25\)
LG d
\(f(x) = {x \over {x + 2}}\) trên nửa khoảng (-2;4]
Lời giải chi tiết:
\(f'(x) = {2 \over {{{\left( {x + 2} \right)}^2}}} > 0\) với mọi \(x \ne 2\).
Hàm số đồng biến trên nửa khoảng \(\left( { - 2;4} \right]\)
BBT:
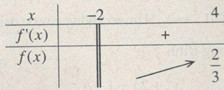
\(\mathop {\max }\limits_{x \in \left( { - 2;4} \right]} f(x) = f(4) = {2 \over 3}\).
Hàm số không đạt giá trị nhỏ nhất trên nửa khoảng \(\left( {-2;4} \right]\).
LG e
\(f(x) = x + 2 + {1 \over {x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\)
Lời giải chi tiết:
\(\begin{array}{l}
f'\left( x \right) = 1 - \frac{1}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{{\left( {x - 1} \right)}^2} - 1}}{{{{\left( {x - 1} \right)}^2}}}\\
f'\left( x \right) = 0 \Leftrightarrow {\left( {x - 1} \right)^2} = 1\\
\Leftrightarrow \left[ \begin{array}{l}
x - 1 = 1\\
x - 1 = - 1
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 2 \in \left( {1; + \infty } \right)\\
x = 0 \notin \left( {1; + \infty } \right)
\end{array} \right.
\end{array}\)
BBT:
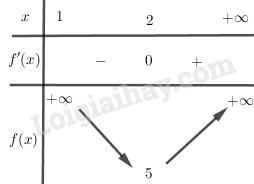
Hàm số không đạt giá trị lớn nhất trên khoảng \(\left( {1; + \infty } \right)\)
\(\mathop {\min f}\limits_{x \in \left( {1; + \infty } \right)} (x) = f(2) = 5\)
LG f
\(f\left( x \right) = x\sqrt {1 - {x^2}} \)
Lời giải chi tiết:
Hàm số xác định và liên tục trên đoạn \(\left[ { - 1;1} \right]\)
\(f'\left( x \right) = \sqrt {1 - {x^2}} - {{{x^2}} \over {\sqrt {1 - {x^2}} }}\)\(= {{1 - 2x^2} \over {\sqrt {1 - {x^2}} }}\) với -1 < x < 1
\(f'\left( x \right) = 0 \Leftrightarrow x = \pm {{\sqrt 2 } \over 2}\)
BBT:
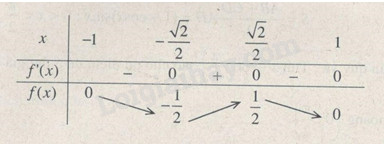
\(\mathop {\min }\limits_{x \in \left( { - 1;1} \right)} f(x) = f( - {{\sqrt 2 } \over 2}) = -{1 \over 2};\)
\(\mathop {m{\rm{ax}}}\limits_{x \in \left( { - 1;1} \right)} {\rm{ }}f(x) = f({{\sqrt 2 } \over 2}) = {1 \over 2}\)

