Cho hàm số
y=x2+mx−1,m≠−1
LG a
Tìm m sao cho đồ thị (C) của hàm số đã cho tiếp xúc với đường thẳng y=−x+7
Lời giải chi tiết:
Ta có: y=x+1+m+1x−1
y′=1−m+1(x−1)2
Đồ thị (C ) tiếp xúc với đường thẳng y=−x+7
⇔ hoành độ tiếp điểm là nghiệm của hệ:
{x+1+m+1x−1=−x+71−m+1(x−1)2=−1⇔{m+1x−1=−2x+6m+1(x−1)2=2⇔{m+1x−1=−2x+61x−1.(−2x+6)=2⇔{m+1x−1=−2x+6−2x+6=2(x−1)⇔{m+1x−1=−2x+6−4x+8=0⇔{x=2m=1
Vậy m=1.
LG b
Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho m = 1.
Lời giải chi tiết:
Với m=1 ta có:
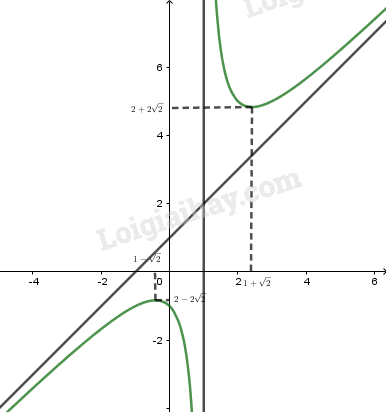
y=x2+1x−1=x+1+2x−1
+) TXĐ: D=R∖{1}
+) Chiều biến thiên:
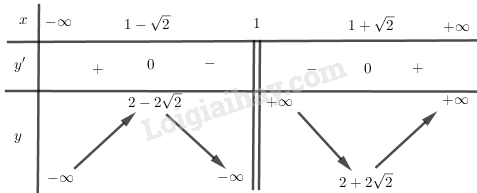
lim nên TCĐ x = 1.
\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \left( {\frac{2}{{x - 1}}} \right) = 0 nên TCX: y = x + 1.
Ta có:
\begin{array}{l}y' = 1 - \frac{2}{{{{\left( {x - 1} \right)}^2}}}\\y' = 0 \Leftrightarrow 1 - \frac{2}{{{{\left( {x - 1} \right)}^2}}} = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} = 2\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = \sqrt 2 \\x - 1 = - \sqrt 2 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1 + \sqrt 2 \\x = 1 - \sqrt 2 \end{array} \right.\end{array}
BBT:
+) Đồ thị: