Cho tam giác ABC vuông ở A, AB = c,AC = b. Trên đường thẳng d vuông góc với mp(ABC) tại A, lấy điểm S bất kì, \(S \ne A\) . Gọi B1, C1 lần lượt là hình chiếu của A trên SB, SC.
LG 1
Xác định tâm của mặt cầu đi qua các điểm A, B, C, B1, C1 và tính bán kính của mặt cầu đó.
Lời giải chi tiết:
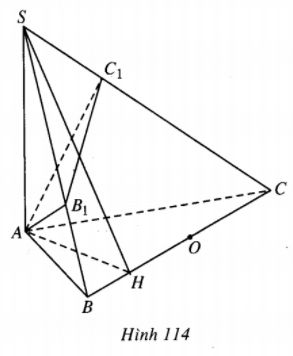
Ta có AC \( \bot \) mp(SAB) nến AC\( \bot \)SB, từ đó SB \( \bot \) B1C tức là \(\widehat {B{B_1}C} = {90^0}\)
Tương tự ta cũng có \(\widehat {B{C_1}C} = {90^0}\). Vậy tâm mặt cầu đi qua B, C, A, B1, C1 là trung điểm O của BC.
Ta có \(AO = {1 \over 2}{\rm{ }}BC,\)
\(B{C^2} = A{B^2} + A{C^2} = {\rm{ }}{b^2} + {\rm{ }}{c^2}.\)
Từ đó bán kính mặt cầu bằng\({{\sqrt {{b^2} + {\rm{ }}{c^2}} } \over 2}.\)
LG 2
Cho SA = h, tính tỉ số thể tích của hai tứ diện SA B1C1 và SABC
Lời giải chi tiết:
Ta có
\({{{V_{S.A{B_1}{C_1}}}} \over {{V_{S.ABC}}}} = {{SA} \over {SA}}.{{S{B_1}} \over {SB}}.{{S{C_1}} \over {SC}} \)
\(= {{S{B_1}.SB} \over {S{B^2}}}.{{S{C_1}.SC} \over {S{C^2}}} = {{S{A^2}} \over {S{B^2}}}.{{S{A^2}} \over {S{C^2}}} = {{{h^4}} \over {\left( {{h^2} + {c^2}} \right)\left( {{h^2} + {b^2}} \right)}}.\)
Vậy tỉ số thể tích của hai tứ diện \(SA{B_1}{C_1}\) và \(SABC\) bằng \({{{h^4}} \over {({h^2} + {b^2})({h^2} + {c^2})}}.\)

