Trong không gian Oxyz cho bốn điểm A(1;1;0), B(0;2;1), C(1;0;2), D(1;1;1).
LG a
Chứng minh bốn điểm đó không đồng phẳng. Tính thể tích tứ diện ABCD.
Lời giải chi tiết:
\(\overrightarrow {AB} = ( - 1;1;1),\overrightarrow {AC} = (0; - 1;2),\overrightarrow {AD} = (0;0;1)\)
Ta có : \(\left[ {\overrightarrow {AB} .\overrightarrow {AC} } \right].\overrightarrow {AD} = 1 \ne 0 \Rightarrow \overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) không đồng phẳng. Do đó bốn điểm A, B, C, D không đồng phẳng và
\({V_{ABCD}} = {1 \over 6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right| = {1 \over 6}.\)
LG b
Tìm tọa độ trọng tâm của tam giác ABC, trọng tâm của tứ diện ABCD.
Lời giải chi tiết:
Gọi G là trọng tâm của tam giác ABC thì \(G = \left( {{2 \over 3};1;1} \right)\)
Gọi G’ là trọng tâm của tứ diện ABCD thì \(G' = \left( {{3 \over 4};1;1} \right)\)
LG c
Tính diện tích các mặt của tứ diện ABCD.
Lời giải chi tiết:
\({S_{ABC}} = {1 \over 2}\left| {\left[ {\overrightarrow {AB} .\overrightarrow {AC} } \right]} \right| \)
\(= {1 \over 2}\sqrt {\left| \matrix{ 1 \hfill \cr - 1 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr 1 \hfill \cr} \right|}^2} + \left| \matrix{ 1 \hfill \cr 2 \hfill \cr} \right.{{\left. \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right|}^2} + \left| \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr - 1 \hfill \cr} \right|}^2}} = {{\sqrt {14} } \over 2}\)
\(\eqalign{ & {S_{ACD}} = {1 \over 2}\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {AD} } \right]} \right|\cr& = {1 \over 2}\sqrt {\left| \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right.{{\left. \matrix{ 2 \hfill \cr 1 \hfill \cr} \right|}^2} + \left| \matrix{ 2 \hfill \cr 1 \hfill \cr} \right.{{\left. \matrix{ 0 \hfill \cr 0 \hfill \cr} \right|}^2} + \left| \matrix{ 0 \hfill \cr 0 \hfill \cr} \right.{{\left. \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right|}^2}} = {1 \over 2}. \cr & {S_{ADB}} = {1 \over 2}\left| {\left[ {\overrightarrow {AD} ,\overrightarrow {AB} } \right]} \right| \cr&= {1 \over 2}\sqrt {\left| \matrix{ 0 \hfill \cr 1 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr 1 \hfill \cr} \right|}^2} + \left| \matrix{ 1 \hfill \cr 1 \hfill \cr} \right.{{\left. \matrix{ 0 \hfill \cr - 1 \hfill \cr} \right|}^2} + \left| \matrix{ 0 \hfill \cr - 1 \hfill \cr} \right.{{\left. \matrix{ 0 \hfill \cr 1 \hfill \cr} \right|}^2}} = {{\sqrt 2 } \over 2}. \cr & {S_{BCD}} = {1 \over 2}\left| {\left[ {\overrightarrow {BC} ,\overrightarrow {BD} } \right]} \right| \cr&= {1 \over 2}\sqrt {\left| \matrix{ - 2 \hfill \cr - 1 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr 0 \hfill \cr} \right|}^2} + \left| \matrix{ 1 \hfill \cr 0 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr 1 \hfill \cr} \right|}^2} + \left| \matrix{ 1 \hfill \cr 1 \hfill \cr} \right.{{\left. \matrix{ - 2 \hfill \cr - 1 \hfill \cr} \right|}^2}} = {{\sqrt 3 } \over 2}. \cr} \)
LG d
Tính độ dài các đường cao của tứ diện ABCD.
Lời giải chi tiết:
Từ công thức tính thể tích khối tứ diện \(V = {1 \over 3}Bh\) (B là diện tích đáy,hlaf chiều cao tương ứng ) ta suy ra \(h = {{3V} \over B}.\)
Vậy nếu gọi \({h_A},{h_B},{h_C},{h_D}\) lần lượt là chiều cao hạ từ đỉnh A, B,C, D thì ta có :
\(\eqalign{ & {h_A} = {{3V} \over {{S_{BCD}}}} = {{3.{1 \over 6}} \over {{{\sqrt 3 } \over 2}}} = {1 \over {\sqrt 3 }},\cr&{h_B} = {{3V} \over {{S_{ACD}}}} = {{3.{1 \over 6}} \over {{1 \over 2}}} = 1. \cr & {h_C} = {{3V} \over {{S_{ABD}}}} = {{3.{1 \over 6}} \over {{{\sqrt 2 } \over 2}}} = {1 \over {\sqrt 2 }},\cr&{h_D} = {{3V} \over {{S_{ABC}}}} = {{3.{1 \over 6}} \over {{{\sqrt {14} } \over 2}}} = {1 \over {\sqrt {14} }}. \cr} \)
LG e
Tính góc giữa hai đường thẳng AB và CD.
Lời giải chi tiết:
Vì \(\overrightarrow {AB} = ( - 1;1;1),\overrightarrow {CD} = (0;1; - 1)\) nên \(\overrightarrow {AB} .\overrightarrow {CD} = 0\), suy ra góc giữa AB và CD bằng 900.
LG g
Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD.
Lời giải chi tiết:
Gọi I(x;y;z) là tâm mặt cầu ngoại tiếp tứ diện ABCD. Khi đó, ta có
\( \left\{ \matrix{ I{A^2} = I{B^2} \hfill \cr I{A^2} = I{C^2} \hfill \cr I{A^2} = ID \hfill \cr} \right.\)
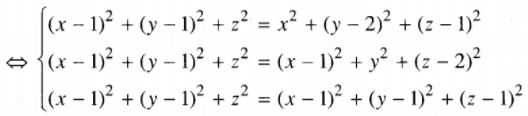
\( \Leftrightarrow \left\{ \matrix{ - 2x + 2y + 2z = 3 \hfill \cr - 2y + 4z = 3 \hfill \cr 2z = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - {3 \over 2} \hfill \cr y = - {1 \over 2} \hfill \cr z = {1 \over 2}. \hfill \cr} \right. \)
Vậy tâm của mặt cầu ngoại tiếp tứ giác ABCD là \(I\left( { - {3 \over 2}; - {1 \over 2};{1 \over 2}} \right)\) và bán kính của mặt cầu đó là
\(R = ID = \sqrt {{{\left( {{5 \over 2}} \right)}^2} + {{\left( {{3 \over 2}} \right)}^2} + {{\left( {{1 \over 2}} \right)}^2}} = {{\sqrt {35} } \over 2}.\)
Do đó, phương trình mặt cầu ngoại tiếp tứ diện ABCD là
\({\left( {x + {3 \over 2}} \right)^2} + {\left( {y + {1 \over 2}} \right)^2} + {\left( {z - {1 \over 2}} \right)^2} = {{35} \over 4}.\)

