Lựa chọn câu để xem lời giải nhanh hơn
Tính diện tích hình phẳng giới hạn bởi:
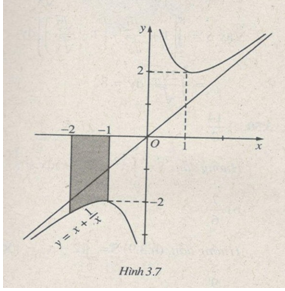
LG a
Đồ thị hàm số y=x+1x, trục hoành, đường thẳng x=−2 và đường thẳng x=−1
Lời giải chi tiết:
S=−1∫−2|1+1x|dx (h.3.7)
=−−1∫−2(1+1x)dx=(−x−ln|x|)|−1−2=1+ln2
LG b
Đồ thị hàm số y=1−1x2, trục hoành, đường thẳng x=1 và đường thẳng x=2
Lời giải chi tiết:
S=2∫1(1−1x2)dx=(x+1x)|21=0,5
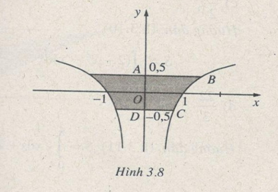
LG c
Đồ thị hàm số y=1−1x2, đường thẳng y=−12 và đường thẳng y=12
Lời giải chi tiết:
Diện tích hình thang cong ABCD là 12∫−12dy√1−y=√6−√2 (h.3.8)
Do đó diện tích hình phẳng cần tìm là: 2(√6−√2)