Cho hàm số
\(y = {{x - 2} \over {x - 1}}\)
LG a
Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số đã cho.
Lời giải chi tiết:
+) TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
+) Chiều biến thiên:
\(\mathop {\lim }\limits_{x \to \pm \infty } y = 1\) nên TCN \(y = 1\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = - \infty ,\mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \) nên TCĐ \(x = 1\)
Ta có:
\(y' = \frac{1}{{{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D\)
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) nên không có cực trị.
BBT:
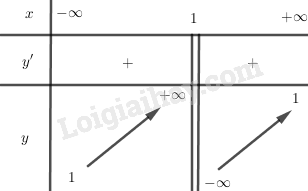
+) Đồ thị:
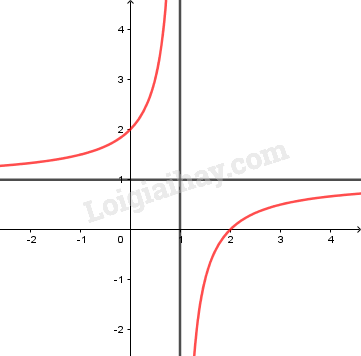
LG b
Chứng minh rằng với mọi \(m \ne 0\), đường thẳng \(y = mx - 3m\) cắt đường cong (H) tại hai điểm phân biệt, trong đó ít nhất một giao điểm có hoành độ lớn hơn 2.
Lời giải chi tiết:
Hoành độ giao điểm của đường thẳng và đường cong (H) là nghiệm của phương trình.
\(mx - 3m = {{x - 2} \over {x - 1}}\)
\( \Leftrightarrow (mx - 3m)(x - 1) = x - 2\)
\( \Leftrightarrow f(x) = m{x^2} - (4m + 1)x + 3m + 2 = 0\) (1)
Vì với mọi \(m \ne 0\)
\(\Delta = {(4m + 1)^2} - 4m(3m + 2) = 4{m^2} + 1 > 0\)
Nên phương trình trên có hai nghiệm phân biệt: \({x_1} = 2 + {{1 - \sqrt {4{m^2} + 1} } \over {2m}}\) và \({x_2} = 2 + {{1 + \sqrt {4{m^2} + 1} } \over {2m}}\).
Do đó, với mọi \(m \ne 0\), đường thẳng cắt đường cong (H) tại hai điểm phân biệt.
- Nếu m < 0 thì \({x_1} > 2\) vì \({{1 - \sqrt {4{m^2} + 1} } \over {2m}} > 0\)
- Nếu m > 0 thì \({x_2} > 2\) vì \({{1 + \sqrt {4{m^2} + 1} } \over {2m}} > 0\)

