Trong không gian Oxyz cho ba điểm A(1;0;0), B(0;0;1) và C(2;1;1).
LG a
Chứng minh A, B, C là ba đỉnh của một tam giác .
Lời giải chi tiết:
Ta có →CA=(−1;−1;−1),→CB=(−2;−1;0)
[→CA,→CB]=(|−1−1−10|;|−10−1−2|;|−1−2−1−1|)
=(−1;2;−1)≠→0
⇒→CA,→CB không cùng phương hay A, B, C không thẳng hàng, tức A, B, C là ba đỉnh của một tam giác.
LG b
Tính chu vi, diện tích tam giác ABC.
Lời giải chi tiết:
Chu vi tam giác ABC bằng AB+BC+CA=√2+√5+√3
SABC=12|[→CA,→CB]|
=12√(−1)2+22+(−1)2=√62.
LG c
Tìm tọa độ điểm D để ABCD là hình bình hành.
Lời giải chi tiết:
Giả sử D = (x,y,z) ta có : →AB=(−1;0;1),→DC=(2−x;1−y;1−z).
Tứ giác ABCD là hình bình hành ⇔→AB=→DC⇔{2−x=−11−y=01−z=1⇒D=(3;1;0).
LG d
Tính độ dài đường cao hA của tam giác ABC kẻ từ A.
Lời giải chi tiết:
Gọi hA là đường cao của tam giác ABC kẻ từ A, ta có :
hA=2SABCBC=√6√5=√305
LG e
Tính các góc của tam giác ABC.
Lời giải chi tiết:
cosA=→AB.→AC|→AB|.|→AC|=0⇒A=900 (tam giác ABC vuông tại A).
cosB=→BA.→BC|→BA|.|→BC|=2√10=√105.cosC=→CA.→CB|→CA|.|→CB|=3√15=√155.
LG g
Xác định tọa độ trực tâm tam giác ABC.
Lời giải chi tiết:
Tam giác ABC vuông tại A nên trực tâm H trùng A. Vậy H=(1;0;0).
Ta có thể làm cách khác như sau :
Gọi H(x;y;z) là trực tâm của tam giác ABC, ta có hệ
{→AH.→BC=0→BH.→AC=0→AB,→AC,→AH đồng phẳng
⇔{→AH.→BC=0→BH.→AC=0[→AB,→AC].→AH=0.
Ta có :
→AH=(x−1;y;z),→BC=(2;1;0),→BH=(x;y;z−1),→AB=(−1;0;1),→AC=(1;1;1)⇒[→AB,→AC]=(−1;2;−1),[→AB,→AC].→AH=1−x+2y−z.
Vậy ta có hệ phương trình :
{2x−2+y=0x+y+z−1=01−x+2y−z=0
⇔{2x+y=2x+y+z=1x−2y+z=1
⇔{x=1y=0z=0⇒H(1;0;0).
LG h
Xác định tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Lời giải chi tiết:
Tam giác ABC vuông tại A nên tâm I của đường tròn ngoại tiếp tam giác là trung điểm của cạnh huyền BC. Do đó I=(1;12;1).
Ta có thể làm cách như sau:
Gọi I(x;y;z) là tâm đường tròn ngoại tiếp ΔABC. Ta có hệ
{AI=BIAI=CI→AB,→AC,→AI đồng phẳng
⇔{AI2=BI2AI2=CI2[→AB,→AC].→AI=0
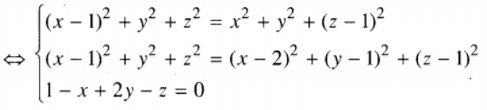
⇔{x=1y=12z=1⇒I(1;12;1).

