Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình thang cân với đáy nhỏ AB = a, đáy lớn CD = 4a, cạnh bên \({{5a} \over 2}\); chiều cao hình lăng trụ bằng h.
LG 1
Chứng minh rằng có hình trụ nội tiếp hình lăng trụ đã cho.
Lời giải chi tiết:
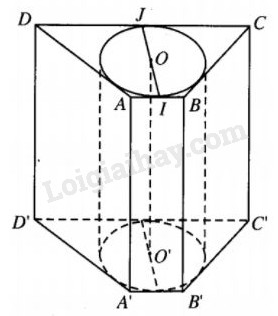
Vì hình lăng trụ đã cho là hình lăng trụ đứng nên chỉ cần chứng minh đáy ABCD có đường tròn nội tiếp.
Gọi I và J lần lượt là trung điểm của AB và CD thì \({\rm{IJ}} \bot AB,IJ \bot CD.\) Gọi O là trung điểm của IJ thì \(OI = {\rm{OJ}} = {{{\rm{IJ}}} \over 2}.\) Kẻ \(BH \bot CD.\)
Ta có \({\rm{IJ}} = BH = \sqrt {B{C^2} - H{C^2}} \)
\( = \sqrt {{{25{a^2}} \over 4} - {{\left( {2a - {a \over 2}} \right)}^2}} = 2a.\)
Vậy OI = OJ = a.

Mặt khác \(O{B^2} = O{I^2} + I{B^2}\)
\(\eqalign{ & \;\;\;\;\;\;\;\; = {a^2} + {{{a^2}} \over 4} = {{5{a^2}} \over 4}, \cr & O{C^2} = {\rm{O}}{{\rm{J}}^2} + J{C^2} \cr & \;\;\;\;\;\;\;\;\;= {a^2} + 4{a^2} = 5{a^2}, \cr} \)
từ đó ta có \(B{C^2} = O{B^2} + O{C^2}.\)
Kẻ đường cao OK của tam giác vuông OBC thì OK.BC = OB.OC, suy ra
\(OK = {{{{a\sqrt 5 } \over 2}.a\sqrt 5 } \over {{{5a} \over 2}}} = a.\)
Vậy O là tâm đường tròn nội tiếp hình thang cân ABCD.
Vậy hình trụ có trục OO’ ( O, O’ là tâm hai đường tròn đáy) và bán kính đáy bằng a chính là hình trụ nội tiếp hình lăng trụ đã cho.
LG 2
Tính diện tích toàn phần và thể tích của hình lăng trụ đó.
Lời giải chi tiết:
Diện tích toàn phần của hình trụ đó là
\(S = 2\pi {a^2} + 2\pi ah = 2\pi a(a + h)\)
Và thể tích hình trụ đó là
\(V = \pi {a^2}h.\)
Chú ý. Có thể giải thích ABCD có đường tròn nội tiếp bởi điều kiện
AB + CD = BC + AD.

