Lựa chọn câu để xem lời giải nhanh hơn
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A(0;0;0), B(a;0;0), D(0;a;0), A’(0;0;b) với a, b là những số dương và M là trung điểm của CC’.
LG a
Tính thể tích của tứ diện BDA’M.
Lời giải chi tiết:
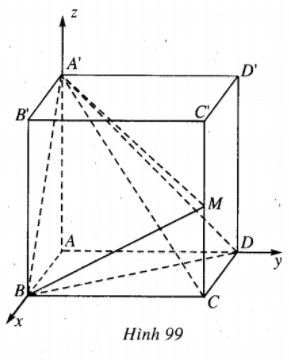
Từ giả thiết ta có C=(a;a;0).
C′=(a;a;b)⇒M=(a;a;b2)
Ta có →BD=(−a;a;0);
→BM=(0;a;b2);→BA′=(−a;0;b)
⇒([→BD,→BM])=(ab2;ab2;−a2)
Vậy VBDA′M=16|[→BD,→BM].→BA′|=a2b4.
LG b
Tìm tỉ số ab để mp(A’BD) vuông góc với mp(MBD).
Lời giải chi tiết:
Mặt phẳng (A’BD) có vec tơ pháp tuyến
→n1=[→BD,→BA′]=(ab;ab;a2).
Mặt phẳng (MBD) có vectơ pháp tuyến
→n2=[→BD,→BM]=(ab2;ab2;−a2).
Vì vậy
(MBD)⊥(A′BD)⇔→n1.→n2=0⇔a2b22+a2b22−a4=0⇔a2b2=a4⇔a2=b2⇔a=b⇔ab=1.
(do a>0,b>0).

