Cho hình chóp S.ABC có đáy ABC là tam giác cân, AB = AC = a ; mp(SBC)\( \bot \)mp(ABC) và SA = SB = a ;
LG 1
Chứng minh rằng SBC là tam giác vuông.
Lời giải chi tiết:
(h.l 12a)
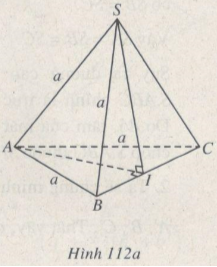
Gọi I là trung điểm của BC, ta có AI \( \bot \) BC. Do (SBC) \( \bot \) (ABC) nên AI \( \bot \) mp(SBC), suy ra \(\Delta \)SAI vuông tại I.
Các tam giác vuông SAI, BAI có IA chung, AB = AS, do đó IB = IS, mặt khác IB = IC, suy ra tam giác SBC vuông ở S.
LG 2
Tính thể tích của khối cầu ngoại tiếp hình chóp S.ABC biết \(SC = {{3a} \over 2}.\)
Lời giải chi tiết:
Vì IB = IC = IS và AI \( \bot \) (SBC) nên tâm O của mặt cầu ngoại tiếp hình chóp S.ABC thuộc đường thẳng AI, suy ra O là tâm đường tròn ngoại tiếp tam giác cân ABC và bán kính R của mặt cầu ngoại tiếp S.ABC cũng là bán kính đường tròn ngoại tiếp tam giác ABC.
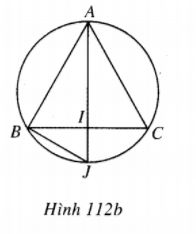
Gọi J là giao điểm thứ hai của AI (h.l 12b) và đường tròn ngoại tiếp tam giác ABC thì AJ = 2R và AB2 = AI.AJ hay a2 = AI.2R
\( \Rightarrow R = {{{a^2}} \over {2AI}}.\) (1)
Mặt khác
\(B{C^2} = S{B^2} + {\rm{ }}S{C^2} = {a^2} + {{9{a^2}} \over 4} = {{13{a^2}} \over 4}\)
Và \(A{I^2} = A{B^2} - B{I^2} = {a^2} - {{B{C^2}} \over 4} \)
\(= {a^2} - {{13{a^2}} \over {16}} = {{3{a^2}} \over {16}} \Rightarrow AI = {{a\sqrt 3 } \over 4}.\) (2)
Thay (2) vào (1) ta có \(R{\rm{ }} = {{2a} \over {\sqrt 3 }}.\)
Vậy thể tích khối cầu ngoại tiếp hình chóp S.ABC là \({4 \over 3}\pi {{8{a^3}} \over {3\sqrt 3 }} = {{32\pi {a^3}} \over {9\sqrt 3 }}.\)

