Tìm cực trị các hàm số sau:
LG a
f(x)=2x3−9x2+12x+3
Lời giải chi tiết:
f′(x)=6x2−18x+12f′(x)=0⇔6x2−18x+12=0⇔[x=1x=2
BBT:
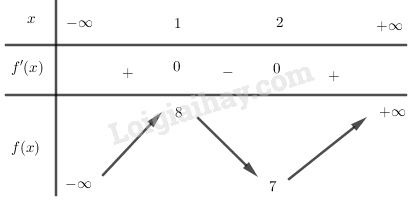
Hàm số đạt cực đại tại điểm x = 1; f(1) = 8 và đạt cực tiểu tại điểm x = 2; f(2) = 7
LG b
f(x)=−5x3+3x2−4x+5
Lời giải chi tiết:
f′(x)=−15x2+6x−4
Có Δ′=9−(−15).(−4)=−51<0 và a=−15<0 nên f′(x)<0,∀x∈R
Do đó hàm số nghịch biến trên R nên không có cực trị.
LG c
f(x)=3x4−4x3−24x2+48x−3
Lời giải chi tiết:
f′(x)=12x3−12x2−48x+48f′(x)=0⇔12x3−12x2−48x+48=0⇔x3−x2−4x+4=0⇔x2(x−1)−4(x−1)=0⇔(x−1)(x2−4)=0⇔[x=1x=±2
BBT:
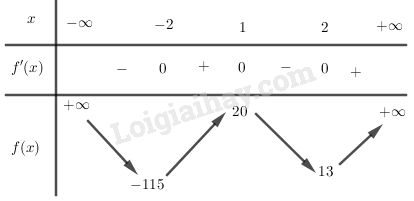
Hàm số đạt cực tiểu tại các điểm x = -2; f(-2) = -115 và x = 2; f(2) = 13.
Đạt cực đại tại điểm x = 1; f(1) = 20.
LG d
f(x)=x−3+9x−2
Lời giải chi tiết:
f′(x)=1−9(x−2)2f′(x)=0⇔1−9(x−2)2=0⇔(x−2)2−9(x−2)2=0⇔(x−2)2=9⇔[x−2=3x−2=−3⇔[x=5x=−1
BBT:
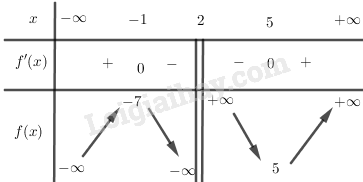
Hàm số đạt cực đại tại điểm x = -1; f(-1) = -7, đạt cực tiểu tại điểm x = 5; f(5) = 5.

