LG a
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
\(f(x) = {{{x^2} - 1} \over x}\)
Lời giải chi tiết:
Ta có: \(f\left( x \right) = \frac{{{x^2} - 1}}{x} = x - \frac{1}{x}\)
+) TXĐ: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
+) Chiều biến thiên:
\(\mathop {\lim }\limits_{x \to {0^ + }} y = - \infty ,\mathop {\lim }\limits_{x \to {0^ - }} y = + \infty \) nên TCĐ: \(x = 0\).
\(\mathop {\lim }\limits_{x \to \pm \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( { - \frac{1}{x}} \right) = 0\) nên TCX: \(y = x\).
Ta có:
\(y' = 1 + \frac{1}{{{x^2}}} > 0,\forall x \in D\)
Hàm số đồng biến trên từng khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\) và không có cực trị.
BBT:
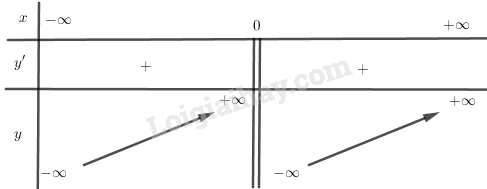
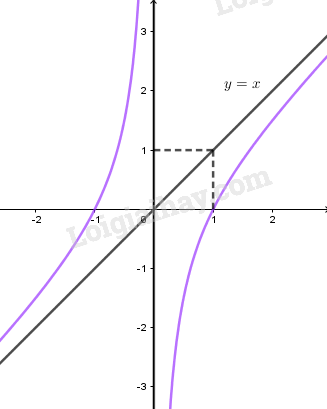
+) Đồ thị:
Đồ thị hàm số cắt trục hoành tại các điểm \(\left( { - 1;0} \right)\) và \(\left( {1;0} \right)\).
LG b
Viết phương trình tiếp tuyến của đường cong (C) tại điểm \(M\left( {{x_0};{f_{\left( {{x_0}} \right)}}} \right)\)
Lời giải chi tiết:
Với \(x = {x_0}\) ta có \(f\left( {{x_0}} \right) = {x_0} - \frac{1}{{{x_0}}}\)
\(f'\left( {{x_0}} \right) = 1 + \frac{1}{{x_0^2}}\) nên phương trình tiếp tuyến tại \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là:
\(\begin{array}{l}y = \left( {1 + \frac{1}{{x_0^2}}} \right)\left( {x - {x_0}} \right) + {x_0} - \frac{1}{{{x_0}}}\\ \Leftrightarrow y = \left( {1 + \frac{1}{{x_0^2}}} \right)x - {x_0} - \frac{1}{{{x_0}}} + {x_0} - \frac{1}{{{x_0}}}\\ \Leftrightarrow y = \left( {1 + \frac{1}{{x_0^2}}} \right)x - \frac{2}{{{x_0}}}\end{array}\)
Vậy \(y = \left( {1 + \frac{1}{{x_0^2}}} \right)x - \frac{2}{{{x_0}}}\).
LG c
Tiếp tuyến đó cắt tiệm cận đứng và tiệm cận xiên của (C) theo thứ tự tại hai điểm A và B. Chứng minh rằng M là trung điểm của đoạn thẳng AB và diện tích tam giác OAB không phụ thuộc vào vị trí của điểm M trên đường cong (C).
Lời giải chi tiết:
Hoành độ của điểm B là nghiệm của phương trình
\(\left( {1 + {1 \over {x_0^2}}} \right)x - {2 \over {{x_0}}} = x \)
\( \Leftrightarrow \frac{1}{{x_0^2}}x = \frac{2}{{{x_0}}} \Leftrightarrow x = 2{x_0}\)
\(\Rightarrow {x_B} = 2{x_0}\)
Vì \({x_A} + {x_B} = 0 + 2{x_0} = 2{x_M}\) , và ba điểm A, M, B thẳng hàng nên M là trung điểm của đoạn thẳng AB.
Dễ thấy \({y_A} = - {2 \over {{x_0}}}\)
Diện tích tam giác OAB là
\(S = {1 \over 2}\left| {{y_A}} \right|\left| {{y_B}} \right| \)
\(= {1 \over 2}.{2 \over {\left| {{x_0}} \right|}}.2\left| {{x_0}} \right| = 2\)

