LG a
Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số
y=2x+1x+1
Lời giải chi tiết:
+) TXĐ: D=R∖{−1}
+) Chiều biến thiên:
y′=2−1(x+1)2=1(x+1)2>0, ∀x∈D
Hàm số đồng biến trên mỗi khoảng (−∞;−1) và (−1;+∞).
lim nên TCN: y = 2
\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty ,\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty nên TCĐ: x = - 1.
BBT:
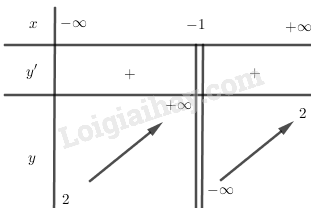
+) Đồ thị:
Cắt trục hoành tại \left( { - \frac{1}{2};0} \right), cắt trục tung tại \left( {0;1} \right).
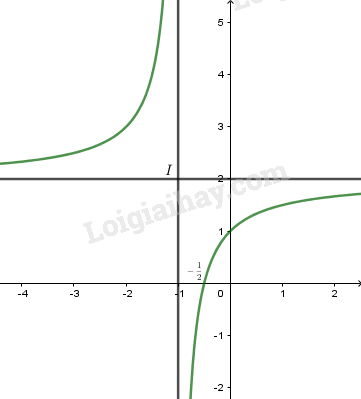
LG b
Chứng minh rằng (H) nhận giao điểm I của hai đường tiệm cận của đồ thị làm tâm đối xứng.
Lời giải chi tiết:
Công thức chuyển hệ tọa độ theo véc tơ \overrightarrow {OI} là: \left\{ \begin{array}{l}x = X - 1\\y = Y + 2\end{array} \right.
Phương trình đường cong trong hệ tọa độ IXY là:
\begin{array}{l}Y + 2 = \frac{{2\left( {X - 1} \right) + 1}}{{X - 1 + 2}}\\ \Leftrightarrow Y + 2 = \frac{{2X - 1}}{X}\\ \Leftrightarrow Y + 2 = 2 - \frac{1}{X}\\ \Leftrightarrow Y = - \frac{1}{X}\end{array}
Đây là hàm số lẻ nên đồ thị nhận I làm tâm đối xứng.

