Cho hình lập phương ABCD.A’B’C’D’ có cạnh 1. Gọi M, N, P lần lượt là trung điểm của các cạnh B’B, CD và A’D’.
LG a
Tính khoảng cách giữa cặp đường thẳng A’B, B’D và cặp đường thẳng PI, AC’ (I là tâm của đáy ABCD).
Lời giải chi tiết:
Ta chọn hệ trục Oxyz sao cho gốc toa độ là A, Tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA’(h.103).
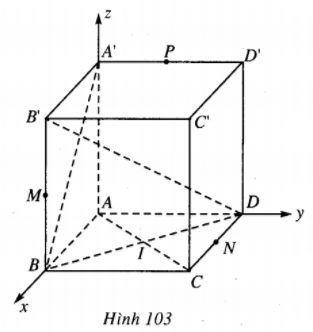
Khi đó
A=(0;0;0),B=(1;0;0)D=(0;1;0),A′=(0;0;1)C=(1;1;0),B′=(1;0;1)C′=(1;1;1),D′=(0;1;1).
Suy ra →A′B=(1;0;−1)
→B′D=(−1;1;−1)
⇒[→A′B,→B′D]=(1;2;1).
→A′B′=(1;0;0)
d(A′B,B′D)=|[→A′B,→B′D].→A′B′||[→A′B,→B′D]|=1√6.
Ta lại có :
P=(0;12;1),I=(12;12;0),→IP=(−12;0;1).→AC′=(1;1;1),→AP=(0;12;1)
Suy ra d(PI,AC′)=|[→IP,→AC′].→AP||[→IP,→AC′]|=√1428.
LG b
Tính góc giữa hai đường thẳng MP và C’N.
Tính góc giữa hai mặt phẳng (PAI) và (DCC’D’).
Lời giải chi tiết:
Ta có M=(1;0;12),N=(12;1;0)
⇒→MP=(−1;12;12),→NC′=(12;0;1)⇒→MP.→NC′=0⇒MP⊥NC′.
Mặt phẳng (PIA) có vectơ pháp tuyến: →n=[→AP,→AI]=(−12;12;−14).
Mặt phẳng (DCC’D’) có vectơ pháp tuyến là →AD=(0;1;0).
Gọi φ là góc giữa hai mặt phẳng trên thì
cosφ=|→n.→AD||→n|.|→AD|=23.

