Cho hình nón tròn xoay đỉnh S, đáy là đường tròn tâm O. Gọi A là điểm cố định và M là điểm thay đổi cùng thuộc đường tròn đáy hình nón. Đặt
AOM=α . Gọi P là góc giữa mp(SAM) và mặt phẳng chứa đáy hình nón ; khoảng cách từ O đến mp(SAM) bằng a.
LG 1
Tính thể tích khối nón đã cho theo a, α,β.
Lời giải chi tiết:
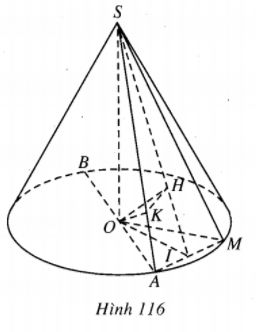
Gọi I là trung điểm của AM thì OI ⊥AM và SI ⊥AM từ đó ^SIO=β. Gọi H là hình chiếu của O trên SI thì OH ⊥ mp(SAM), từ đó OH = a.
Ta có OI=OHsinβ=asinβ.
OM=OIcosα2=asinβcosα2.
SO=OItanβ=asinβ.tanβ=acosβ.
Từ đó thể tích khối nón đã cho là
V=πa33cos2α2sin2βcosβ.
LG 2
Xác định điểm M để tam giác SAM có diện tích lớn nhất.
Lời giải chi tiết:
Ta có
Vì SA không đổi nên SΔSAM lớn nhất ⇔sin^ASM lớn nhất.
Dễ thấy ^ASB>^ASM (B là điểm đối xứng của A qua O). Vậy có hai trường hợp :
a) 0<^ASB<900 Khi đó , sin^ASM≤sin^ASB từ đó sin^ASM lớn nhất khi và chỉ khi M trùng với B.
b) 900<^ASB<1800 Khi đó sin^ASM lớn nhất khi và chỉ khi ^ASM=900. Vậy có hai vị trí của M trên đường tròn đáy hình nón để diện tích tam giác SAM lớn nhất, đó là hai điểm M sao cho ^ASM=900
LG 3
Chứng minh rằng hình chiếu H của điểm O trên mp(SAM) thuộc một đường tròn cố định.
Lời giải chi tiết:
Vì OH ⊥ mp(SAM) nên OH ⊥ SA. Vậy H thuộc mp(P) đi qua O và vuông góc với SA tại K. Ta có (P) là mặt phẳng cố định, ngoài ra ^OHK=900, tức là H thuộc đường tròn đường kính OK trong mặt phẳng (P) nêu trên, tất nhiên đường tròn này cố định.

