Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, ˆB = 600. Biết rằng có một hình nón nội tiếp hình chóp đã cho với bán kính đáy là r, góc giữa đường sinh và đáy hình nón là β.
LG 1
Tính diện tích xung quanh và thể tích hình nón.
Lời giải chi tiết:
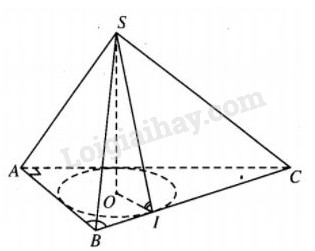
Đáy hình nón trong bài toán là đường tròn nội tiếp tam giác ABC.
Đường cao hình nón là SO (S là đỉnh của hình chóp ).
Gọi I là điểm tiếp xúc của BC với đường tròn nội tiếp ΔABC thì OI⊥BC và SI⊥BC nên ^SIO =β.
Khi đó, chiều cao hình nón là
h=SO=OItanβ=rtanβ,
Độ dài đường sinh hình nón là
l=SI=OIcosβ=rcosβ.
Vậy diện tích xung quanh của hình nón là
S1=πrl=πr.rcosβ=πr2cosβ.
Thể tích hình nón là
V1=13πr2h=13πr2.r.tanβ=13πr3tanβ.
LG 2
Tính diện tích xung quanh và thể tích hình chóp.
Lời giải chi tiết:
Dễ thấy ba đường cao của ba mặt bên hình chóp S.ABC bằng nhau và cùng bằng SI.
Diện tích xung quanh của hình chóp là
S2=12(AB+AC+BC).SI
Mặt khác AC=AB√3,BC=2AB,
SΔABC=12AB.AC=12AB2√3,SΔABC=12(AB+AC+BC).r=12(3+√3).AB.r.
Từ đó AB=(√3+1)r.
Vậy diện tích xung quanh của hình chóp S.ABC là
S2=12(3+√3)AB.SI=12(3+√3)(√3+1)r.rcosβ=√32(√3+1)2r2cosβ.
Thể tích hình chóp S.ABC là
V2=13.12AB.AC.SO=√36AB2.SO, từ đó
V2=√36(√3+1)2r2.rtanβ=√36(√3+1)2r3tanβ.

