LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số
y=−x3+32x2+6x−3
Lời giải chi tiết:
+) TXĐ: D=R.
+) Chiều biến thiên:
limx→+∞y=−∞,limx→−∞y=+∞
y′=−3x2+3x+6y′=0⇔−3x2+3x+6=0⇔[x=−1x=2
BBT:
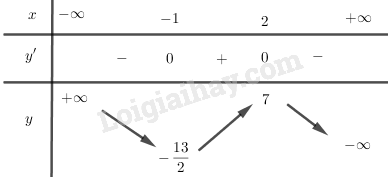
Hàm số nghịch biến trên (−∞;−1) và (2;+∞).
Hàm số đồng biến trên (−1;2).
Hàm số đạt cực đại tại x=2,yCD=7
Hàm số đạt cực tiểu tại x = - 1,{y_{CT}} = - \frac{{13}}{2}.
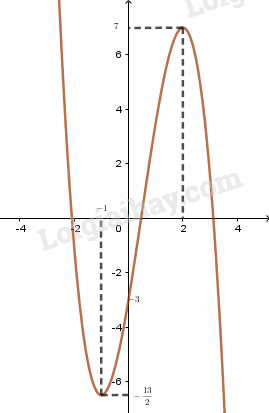
+) Đồ thị:
\begin{array}{l}y'' = - 6x + 3\\y'' = 0 \Leftrightarrow - 6x + 3 = 0\\ \Leftrightarrow x = \frac{1}{2} \Rightarrow y\left( {\frac{1}{2}} \right) = \frac{1}{4}\end{array}
Điểm uốn I\left( {\frac{1}{2};\frac{1}{4}} \right).
Đồ thị hàm số cắt trục tung tại điểm \left( {0; - 3} \right).
Điểm cực đại \left( {2;7} \right) và điểm cực tiểu \left( { - 1; - \frac{{13}}{2}} \right).
LG b
Chứng minh rằng phương trình
- {x^3} + {3 \over 2}{x^2} + 6x - 3 = 0
Có ba nghiệm phân biệt, trong đó có một nghiệm dương nhỏ hơn {1 \over 2}.
Lời giải chi tiết:
Quan sát đồ thị của hàm số, dễ dàng thấy rằng phương trình đã cho có ba nghiệm {x_1},{x_2},{x_3} , trong đó {x_1} < - 1,{x_2} \in \left( { - 1;2} \right) và {x_3} > 2 .
Hơn nữa, vì f(0) = - 3 < 0 và f\left( {{1 \over 2}} \right) = {1 \over 4} > 0 nên {x_2} \in \left( {0;{1 \over 2}} \right)

