Cho hai điểm cố định A, B có AB = a. Với mỗi điểm C trong không gian sao cho ABC là tam giác đều, kí hiệu AA1 là đường cao của \(\Delta ABC\) và d là trục của đường tròn ngoại tiếp tam giác ABC. Trong mặt phẳng chứa d và AA1, xét đường tròn đường kính AA1 ; gọi S là một giao điểm của đường tròn này và đường thẳng d.
LG 1
Tính dện tích xung quanh và thể tích hình nón ngoại tiếp hình chóp S.ABC.
Lời giải chi tiết:
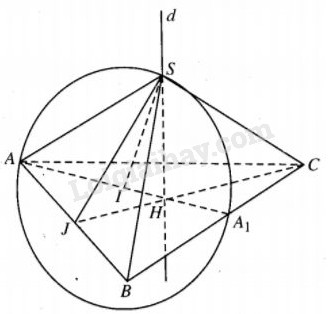
Hình nón ngoại tiếp hình chóp S.ABC có đỉnh S, đáy là đường tròn ngoại tiếp tam giác ABC, đường cao là SH, đường kính là SC.
Gọi Sxq là diện tích xung quanh của hình nón thì \({S_{xq}} = \pi .HC.SC.\)
Ta có \(HC = {{a\sqrt 3 } \over 3},\)
\(S{C^2} = S{H^2} + H{C^2} = S{H^2} + {{{a^2}} \over 3}\)
\( = S{I^2} - I{H^2} + {{{a^2}} \over 3}\) (I là trung điểm của AA1).
Vì S thuộc đường tròn đường kính AA1 nên \(SI = {{a\sqrt 3 } \over 4},\) ngoài ra
\(IH = AH - AI = {{a\sqrt 3 } \over 3} - {{a\sqrt 3 } \over 4} = {{a\sqrt 3 } \over {12}}\)
Vậy \(S{C^2} = {\left( {{{a\sqrt 3 } \over 4}} \right)^2} - {\left( {{{a\sqrt 3 } \over {12}}} \right)^2} + {{{a^2}} \over 3} = {{{a^2}} \over 2},\) tức là \(SC = {{a\sqrt 2 } \over 2}.\)
Vậy \({S_{xq}} = \pi .{{a\sqrt 3 } \over 3}.{{a\sqrt 2 } \over 2} = \pi {{{a^2}\sqrt 6 } \over 6}.\)
Gọi V là thể tích hình nón nêu trên thì
\(\eqalign{ & V = {1 \over 3}\pi .H{C^2}.SH = {1 \over 3}\pi {{{a^2}} \over 3}\sqrt {S{I^2} - I{H^2}} \cr & = {1 \over 9}\pi {a^2}\sqrt {{{3{a^2}} \over {16}} - {{3{a^2}} \over {{{12}^2}}}} = {1 \over 9}\pi .a^2{{a\sqrt 6 } \over 6} \cr & = {{\pi {a^3}\sqrt 6 } \over {54}}. \cr} \)
LG 2
Chứng minh rằng khi điểm C thay đổi thì điểm S thuộc một đường tròn cố định và mỗi đường thẳng SA, SB thuộc một mặt nón cố định.
Lời giải chi tiết:
Gọi J là trung điểm của AB thì \(CJ \bot AB\), do\(SH \bot \left( {ABC} \right)\) nên \(SJ \bot AB.\)
Vậy S thuộc mặt phẳng trung trực của AB. Mặt khác
\(S{J^2} = S{H^2} + H{J^2} = S{I^2} - I{H^2} + H{J^2}\)
\(= {\left( {{{a\sqrt 3 } \over 4}} \right)^2} - {\left( {{{a\sqrt 3 } \over {12}}} \right)^2} + {\left( {{{a\sqrt 3 } \over 6}} \right)^2} = {{{a^2}} \over 4}.\)
Từ đó \(JS = {a \over 2}.\)
Vậy S thuộc đường tròn (\(\Gamma \)) tâm J, bán kính JS nằm trong mặt phẳng trung trực của AB. Dĩ nhiên đường tròn này cố định.
Vì S nằm trên đường tròn (\(\Gamma \)) tâm J và AJ vuông góc với mặt phẳng chứa đường tròn này nên AS thuộc mặt nón nhận (\(\Gamma \)) làm đường tròn đáy và trục AJ (đỉnh A).
Tương tự, BS thuộc mặt nón có đáy là đường tròn (\(\Gamma \)), trục là BJ (đỉnh B).
