Cho hai tia Ax, By chéo nhau và vuông góc với nhau, AB là đường vuông góc chung, AB = a. Lấy các điểm C và D lần lượt thuộc Ax, By.
LG a
Xác định tâm và bán kính mạt cầu ngoại tiếp tứ diện ABCD theo a, b, c ở đó b = AC, c = BD.
Lời giải chi tiết:
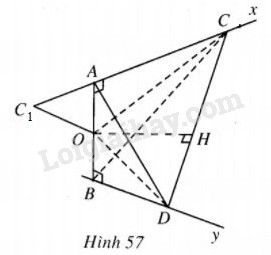
Vì AC⊥AB,AC⊥BD nên AC⊥AD.
Tương tự như trên, ta có CB⊥BD
Vậy CD là đường kính của mặt cầu ngoại tiếp tứ diện ABCD.
Dễ thấy CD2=CA2+AB2+BD2
=a2+b2+c2
Vậy tâm mặt cầu ngoại tiếp tứ diện ABCD là trung điểm của CD và bán kính mặt cầu bằng 12√a2+b2+c2.
LG b
Khi C, D thay đổi trên Ax, By sao cho AC + BD = CD, chứng tỏ rằng CD luôn tiếp xúc với mặt cầu đường kính AB.
Lời giải chi tiết:
Gọi C1 là điểm thuộc tia đối của tia Ax sao cho AC1 = BD.
Gọi O là trung điểm của AB thì
OC21=AC21+AB24,OD2=BD2+AB24,
Do đó OC1 = OD.
Mặt khác CD = AC + BD, từ đó CD = CC1.
Vậy hai tam giác OC1C và ODC bằng nhau, suy ra OA = OH (trong đó OA, OH lần lượt là đường cao của hai tam giác đó).
Điều này khẳng định khoảng cách từ O đến CD bằng AB2, tức là mặt cầu đường kính AB tiếp xúc với CD.

