Đề bài
Lấy một mặt phẳng vuông góc với cạnh bên của một khối lăng tru. Hình chiếu của mặt đáy của khối lăng trụ trên mặt phẳng đó được gọi là thiết diện thẳng của khối lăng trụ.
Chứng minh rằng thể tích của khối lăng trụ bằng tích của diện tích thiết diện thẳng với độ dài cạnh bên.
Lời giải chi tiết
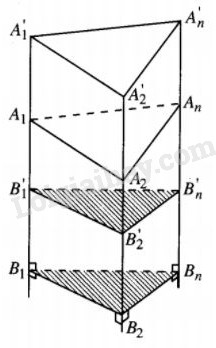
Giả sử khối lăng trụ A1A2...An.A′1A′2...A′n có thiết diện thẳng là B1B2...Bn. Ta có thể lấy B1,B2,...,Bnsao cho các đoạn thẳng B1A1,B2A2,...,BnAn đều lớn hơn A1A′1.
Tịnh tiến khối đa diện B1B2...Bn.A1A2...An theo vectơ →v=→A1A′1, ta được khối đa diện B′1,B′2,...,B′n.A′1A′2...A′n. Hai khối này rõ ràng có thể tích bằng nhau ( do chúng bằng nhau ) và có phần chung là khối đa diện A1A2...An.B′1,B′2,...,B′n. Do đó, thể tích khối lăng trụ A1A2...An.A′1A′2...A′n bằng thể tích khối lăng trụ đứng B1B2...Bn.B′1,B′2,...,B′n.
Vậy nếu gọi V là thể tích của khối lăng trụ đã cho thì
V=SB1B2...Bn.B1B′1=SB1B2...Bn.A1A′1
(B1B′1=A1A′1vì →B1B′1=→A1A′1=→v).
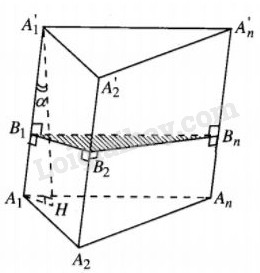
Hạ →A′1H⊥(A1A2...An) thì A′1H bằng chiều cao h của khối lăng trụ.
Khi đó góc giữa mặt phẳng chứa thiết diện thẳng B1B2...Bn và mặt phẳng đáy của khối lăng trụ bằng góc giữa hai đường thẳng A1A′1và A′1H.
Gọi góc này là α thì h=A′1H=A1A′1cosα.
Ta có thiết diện thẳng B1B2...Bn là hình chiếu của đa giác đáy A1A2...An trên mp(B1B2...Bn).
Vậy thể tích của khối lăng trụ là :
V=SA1A2...An.A′1H=SB1B2...BncosαA1A′1cosα=SB1B2...Bn.A1A′1(đpcm).
Loigiaihay.com

