Cho hàm số y=2x2+3x+3x+1
LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
Lời giải chi tiết:
Ta có: y=2x2+3x+3x+1=2x+1+2x+1
+) TXĐ: D=R∖{−1}
+) Chiều biến thiên:
lim nên TCĐ x = - 1.
\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \left( {\frac{2}{{x + 1}}} \right) = 0 nên TCX: y = 2x + 1.
Ta có:
\begin{array}{l}y' = 2 - \frac{2}{{{{\left( {x + 1} \right)}^2}}}\\y' = 0 \Leftrightarrow 2 - \frac{2}{{{{\left( {x + 1} \right)}^2}}} = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 1\\x + 1 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\end{array}
BBT:
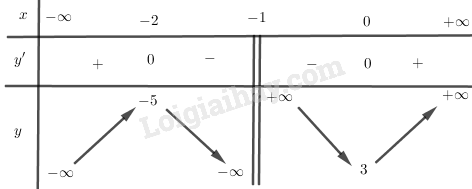
+) Đồ thị:
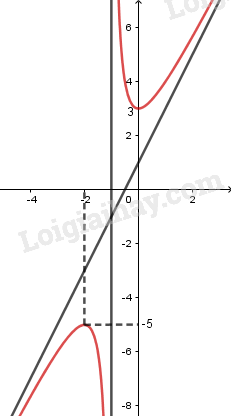
LG b
Dựa vào đồ thị, hãy biện luận số giao điểm của đường thẳng y = m(x + 1) + 3 và đường cong (C), tùy theo các giá trị của m.
Lời giải chi tiết:
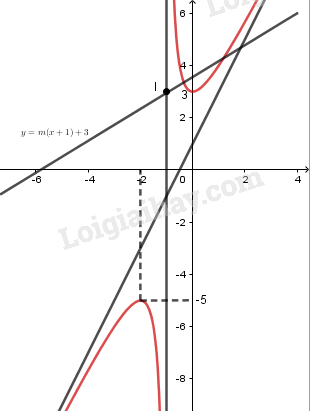
Đường thẳng y = m(x + 1) + 3 có hệ số góc m, đi qua điểm I(-1;3) nằm trên tiệm cận đứng x = -1 của (C).
- Với m < 0 đường thẳng không cắt đường cong (C)
- Với m = 0 đường thẳng tiếp xúc với (C) tại điểm (0;3)
- Với 0 < m < 2 đường thẳng cắt (C) tại hai điểm (cả hai giao điểm đều phải thuộc nhánh phải của (C)
- Với m = 2, đường thẳng song song với tiệm cận xiên của (C); đường thẳng cắt (C) tại một điểm.
- Với m > 2, đường thẳng cắt (C) tại hai điểm thuộc hai nhánh của (C).

