Lựa chọn câu để xem lời giải nhanh hơn
Cho khối lăng trụ tứ giác đều ABCD.A1B1C1D1 có khoảng cách giữa hai đường thẳng AB và A1D bằng 2 và độ dài đường chéo của mặt bên bằng 5.
LG a
Hạ AK⊥A1D(K∈A1D). Chứng minh rằng AK=2.
Lời giải chi tiết:
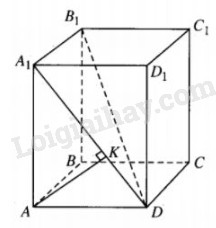
AB//A1B1⇒AB//(A1B1D)⇒d(A,(A1B1D))=d(AB,A1D).
Ta có :
A1B1⊥(AA1D1D)⇒A1B1⊥AK.
Mặt khác A1D⊥AK, suy ra AK⊥(A1B1D)
Vậy AK=d(A,(A1B1D))=d(AB,A1D)=2
LG b
Tính thể tích khối lăng trụ ABCD.A1B1C1D1.
Lời giải chi tiết:
Xét tam giác vuông A1AD, ta có :
AK2=A1K.KD.
Đặt A1K = x 4=x(5−x)⇒x2−5x+4=0
⇒[x=1x=4
Với x=1, AD=√AK2+KD2=2√5
AA1=√A1D2−AD2=√5
Khi đó VABCD.A1B1C1D1=20√5
Với x=4, tương tự ta có :VABCD.A1B1C1D1=10√5.

