Cho hình nón đỉnh S có bán kính đáy R, góc ở đỉnh là \(2\alpha ,\;{45^0} < \alpha < {90^0}.\)
LG 1
Tính diện tích xung quanh và thể tích hình nón.
Lời giải chi tiết:
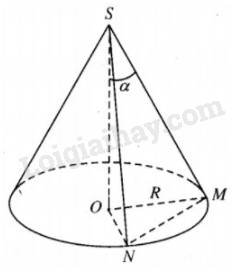
Ta có \(SM = {{OM} \over {\sin \alpha }} = {R \over {\sin \alpha }}\)
\(SO = R\cot \alpha .\)
Diện tích xung quanh của hình nón là
\({S_{xq}} = \pi R.{R \over {\sin \alpha }} = {{\pi {R^2}} \over {\sin \alpha }}.\)
Thể tích khối nón là
\(V = {1 \over 3}\pi {R^2}.R\cot \alpha = {1 \over 3}\pi {R^3}\cot \alpha .\)
LG 2
Tính diện tích thiết diện do mp(P) cắt hình nón theo hai đường sinh vuông góc với nhau.
Lời giải chi tiết:
Giả sử (P) cắt hình nón theo thiết diện SMN và \(SM \bot SN,\) khi đó diện tích thiết diện là
\({S_1} = {1 \over 2}SM.SN = {{{R^2}} \over {2{{\sin }^2}\alpha }}.\)
LG 3
Xét hai điểm A, B thay đổi trên đáy sao cho góc giữa mp(SAB) và mặt đáy hình nón bằng \(\beta\; (\beta < {90^ \circ })\) . Chứng minh rằng đường thẳng SI ( I là trung điểm của AB) luôn thuộc một hình nón cố định.
Lời giải chi tiết:
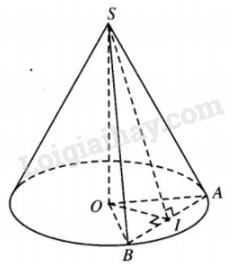
Với I là trung điểm của AB thì \(\widehat {SIO} =\beta ,\)\(OI = SO\cot \beta = R.\cot \alpha .\cot \beta .\)
Vậy điểm I thuộc đường tròn tâm O bán kính \(R.\cot \alpha .\cot \beta \) trong mặt phẳng chứa đáy hình nón.
Vì SI quay quanh S và dựa vào đường tròn tâm O, bán kính \(R.\cot \alpha .\cot \beta \) trong mặt phẳng chứa đáy hình nón đã cho nên SI thuộc một hình nón cố định với đường cao SO, đường tròn đáy của hình nón này là đường tròn đã nêu trên.

