LG a
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
y=−x4−2x2+3
Lời giải chi tiết:
+) TXĐ: D=R
+) Chiều biến thiên:
lim
\begin{array}{l}y' = - 4{x^3} - 4x\\y' = 0 \Leftrightarrow - 4{x^3} - 4x = 0\\ \Leftrightarrow - 4x\left( {{x^2} + 1} \right) = 0\\ \Leftrightarrow x = 0\end{array}
BBT:
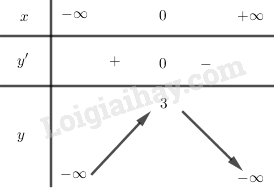
Hàm số đồng biến trên khoảng \left( { - \infty ;0} \right).
Hàm số nghịch biến trên khoảng \left( {0; + \infty } \right).
Hàm số đạt cực đại tại x = 0,{y_{CD}} = 3.
+) Đồ thị:
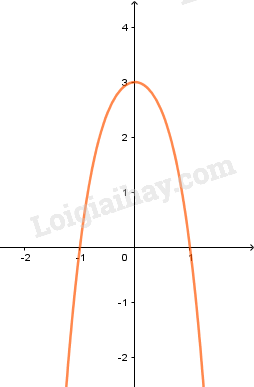
LG b
Với giá trị nào của m, đường thẳng y = 8x + m là tiếp tuyến của đường cong (C)?
Lời giải chi tiết:
Ta có y' = - 4{x^3} - 4x
Hoành độ có tiếp điểm của đường thẳng và đường cong (C) là nghiệm của phương trình
- 4{x^3} - 4x = 8
\eqalign{& \Leftrightarrow {x^3} + x + 2 = 0 \cr & \Leftrightarrow \left( {x + 1} \right)({x^2} - x + 2) = 0\cr& \Leftrightarrow x = - 1 \cr}
M(-1;0) là tiếp điểm của đường thẳng và (C).
Vì điểm M nằm trên đường thẳng nên 8\left( { - 1} \right) + m = 0 .
\Leftrightarrow m = 8

