Đề bài
Cho đường tròn đường kính AB nằm trên mặt phẳng (P) và một điểm M di động trên đường tròn. Trên đường thẳng vuông góc với mp(P) tại A, lấy một điểm S. Mặt phẳng (Q) qua A vuông góc với SB tại K cắt SM tại H. Tìm vị trí của M để tính thể tích khối chóp S.AHK lớn nhất. Chứng minh rằng khi đó cung AM nhỏ hơn cung BM.
Lời giải chi tiết
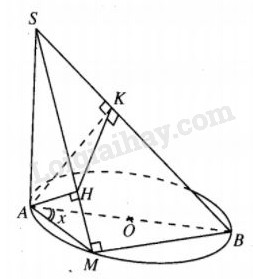
MB⊥AM,MB⊥SA⇒MB⊥(SAM)⇒MB⊥AH(1)SB⊥(AKH)⇒SB⊥AH.(1)
Từ (1) và (2) suy ra AH⊥(SMB)⇒AH⊥SM,AH⊥HK.VS.AHK=13SAHK.SK=16AH.KH.SK.
Vì SK cố định nên :
VS.AHKmax
\Leftrightarrow \left( {A{H^2}.K{H^2}} \right)\max \Leftrightarrow A{H^2} = K{H^2} = {{A{K^2}} \over 2}
( vì A{H^2} + H{K^2} = A{K^2} không đổi).
Vậy ta chỉ cần xác định vị trí điểm M thỏa mãn điều kiện A{H^2} = {{A{K^2}} \over 2}.\left( * \right)
Đặt \widehat {MAB} =x,SA=h, AB=2R. Ta có
\eqalign{ & A{K^2} = {{S{A^2}.A{B^2}} \over {S{B^2}}} = {{4{R^2}{h^2}} \over {4{R^2} + {h^2}}}, \cr & AM = 2R{\mathop{\rm cosx}\nolimits} , \cr & A{H^2} = {{S{A^2}.A{M^2}} \over {S{M^2}}} = {{4{h^2}{R^2}{{\cos }^2}x} \over {{h^2} + 4{R^2}{{\cos }^2}x}}. \cr}
Từ \left( * \right) ta suy ra : {\cos ^2}x = {{{h^2}} \over {2\left( {{h^2} + 2{R^2}} \right)}} < {1 \over 2}.
Từ đây ta xác định được x, tức là xác định được vị trí điểm M (có hai vị trí của điểm M ).
Từ {\cos ^2}x < {1 \over 2} suy ra {\mathop{\rm cosx}\nolimits} < {{\sqrt 2 } \over 2} = \cos {45^0} \Rightarrow x > {45^0} .
Vậy cung BM lớn hơn cung AM

