Đề bài
Một mặt phẳng (α) đi qua hai đường sinh của hình nón, cắt mặt đáy hình nón theo một dây cung có độ dài gấp k lần đường cao hình nón. Tính góc φ giữa mặt phẳng (α) và mặt đáy hình nón nếu φ bằng nửa góc tạo bởi hai đường sinh của hình nón nằm trên mp(α).
Lời giải chi tiết
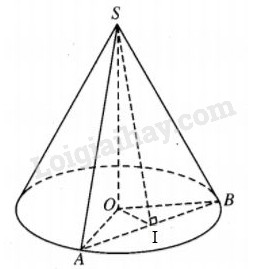
Giả sử O là tâm của đáy hình nón và mặt phẳng (α) đi qua hai đường sinh SA, SB.
Gọi I là trung điểm của AB thì OI⊥AB và SI⊥AB, từ đó ^SIO = φ. Theo giả thiết φ = ^ISB.
Từ tam giác vuông SIO, ta có sinφ=SOSI(1)
Từ tam giác vuông SIB, ta cũng có tanφ=IBSI(2)
Từ (1) và (2) suy ra sinφtanφ=SOIB=SOk2SO=2k.
Vậy cosφ=2k.

