Đề bài
Tìm hình nón có thể tích lớn nhất khi diện tích toàn phần của nó bằng diện tích hình tròn bán kính a cho trước.
Lời giải chi tiết
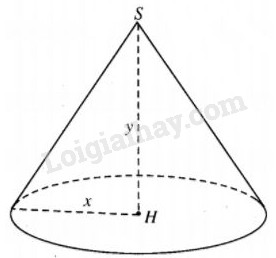
Kí hiệu bán kính đáy và chiều cao hình nón lần lượt là x và y (x, y > 0). Khi đó, diện tích toàn phần của hình nón là
πx√x2+y2+πx2,
Theo gia thiết ta có
πx√x2+y2+πx2=πa2⇔x√x2+y2+x2=a2
⇔x√x2+y2=a2−x2 (điều kiện x < a)
⇔x2(x2+y2)=a4+x4−2a2x2⇔x2y2=a4−2a2x2⇔x2=a4y2+2a2
Khi đó thể tích khối nón là
V=13πa4y2+2a2.y=πa43.yy2+2a2.
Từ đó V đạt giá trị lớn nhất khi và chỉ khi y2+2a2y đạt giá trị nhỏ nhất.
Ta có y2+2a2y=y+2a2y≥2√y.2a2y=2√2a.
Vậy V đạt giá trị lớn nhất khi và chỉ khi y=2a2y, tức là y=a√2, lúc đó x=a2.

