Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng 1.
LG a
Tính góc tạo bởi các đường thẳng AC’ và A’B.
Lời giải chi tiết:
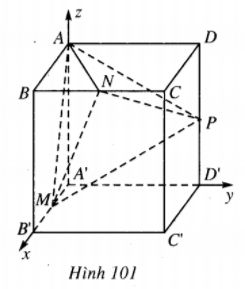
Ta chọn hệ trục Oxyz sao cho gốc O là đỉnh A’ của hình lập phương, tia Oy chứa A’B’, tia Oy chứa A’D’ và tia Oz chứa AA’. Khi đó
A’(0;0;0), B’(1;0;0);
D’(0;1;0), A=(0;0;1);
C=(1;1;1), B=(1;0;1);
D=(0;1;1), C’(1;1;0).
Từ đó :
→AC′=(1;1;−1),→A′B=(1;0;1)⇒→AC′.→A′B=0⇒AC′⊥A′B.
LG b
Gọi M, N, P lần lượt là trung điểm của các cạnh A’B’, BC, DD’. Chứng minh AC’ vuông góc với mặt phẳng (MNP).
Lời giải chi tiết:
Ta có
M=(12;0;0),N=(1;12;1),P=(0;1;12).→MN=(12;12;1)⇒→MN.→AC′=0⇒MN⊥AC′.→MP=(−12;1;12)⇒→MP.→AC′=0⇒MP⊥AC′.
Vậy AC′⊥mp(MNP).
LG c
Tính thể tích tứ diện AMNP.
Lời giải chi tiết:
Ta có : →MA=(−12;0;1).[→MN,→MP]=(|121112|;|11212−12|;|12−12121|)=(−34;−34;34)⇒VAMNP=16|[→MN,→MP].→MA|=16.|98|=316.

