Đề bài
Cho hai đường thẳng chéo nhau a, b và hai đường thẳng chéo nhau a', b'. Biết rằng :
i) Khoảng cách giữa a và b bằng khoảng cách giữa a' và b'
ii) Góc hợp bởi a và b bằng góc hợp bởi a' và b'
Chứng minh rằng có phép dời hình biến a thành a', biến b thành b'.
Lời giải chi tiết
(h.106)
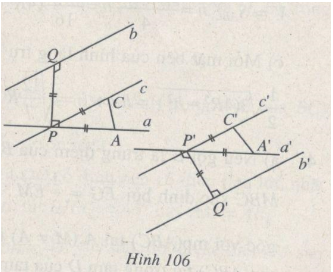
Gọi PQ là đường vuông góc chung của a và b, trong đó\(P \in a,Q{\rm{ }} \in {\rm{ }}b\). Gọi P'Q' là đường vuông góc chung của a' và b' trong đó \(P' \in a',Q' \in {\rm{ }}b'\). Theo giả thiết PQ = P'Q'
Gọi c là đường thẳng đi qua P và song song với b, c' là đường thẳng đi qua P ' và song song với b'. Theo giả thiết, góc giữa a và c bằng góc giữa a' và c'.
Lấy lần lượt trên a và c các điểm A, C sao cho PA = PC = PQ, rồi lấy lần lượt trên a' và c' các điểm A', C' sao cho P'A' = P'C' = P'Q' và góc APC bằng góc A'P'C'. Từ đó, dễ thấy hai tứ diện PQAC và P'Q'A'C' có các cạnh tương ứng bằng nhau.
Vậy có một phép dời hình biến tứ diện PQAC thành tứ diện P'Q'A'C'. Khi đó, biến hai đường thẳng a, b lần lượt thành hai đường thẳng a' và b'
