Đề bài
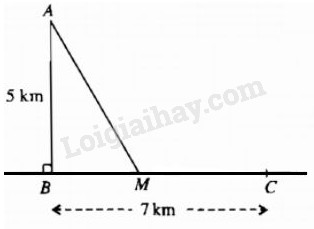
Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng AB = 5km. Trên bờ biền có một cái kho ở vị trí C cách B một khoảng là 7km. Người canh hải đăng có thể chèo đò từ A đến điểm M trên bờ biển với vận tốc 4 km/h rồi đi bộ đến C với vận tốc 6km/h (h.1.5).
Xác định vị trí của điểm M để người đó đến kho nhanh nhất.
Lời giải chi tiết
Đặt x=BM,0≤x≤7.
Khi đó, AM=√x2+25,MC=7−x.
Thời gian người canh hải đăng đi từ A đến C là
T(x)=√x2+254+7−x6 (giờ) 0≤x≤7
Ta tìm x∈[0;7] để T đạt GTNN như sau:
T′(x)=14.x√x2+25−16T′(x)=0⇔14.x√x2+25−16=0⇔14.x√x2+25=16⇔3x=2√x2+25⇔9x2=4x2+100⇔x2=20⇔[x=2√5∈[0;7]x=−2√5∉[0;7]
Hàm số T đạt giá trị nhỏ nhất tại điểm x=2√5≈4,472(km)

