Đề bài
Cho khối hộp ABCD.A1B1C1D1 tất cả các cạnh bằng nhau và bằng a, góc ^A1AB=^BAD=^A1AD=α (00<α<900). Hãy tính thể tích của khối hộp.
Lời giải chi tiết
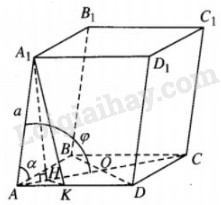
Hạ A1H⊥AC(H∈AC)(∗).
Tam giác A1BD cân ( do A1B=A1D) suy ra BD⊥A1O. Mặt khác
BD⊥AC⇒BD⊥(A1AO)⇒BD⊥A1H(∗∗).
Từ (∗) và (∗∗)⇒A1H⊥(ABCD).
Đặt ^A1AO=φ. Ta có hệ thức :
cosα=cosφ.cosα2
Thật vậy, hạ A1K⊥AD⇒HK⊥AK (định lý ba đường vuông góc )
⇒cosφ.cosα2=AHAA1.AKAH=AKAA1=cosα.
Từ đẳng thức trên ta suy ra : cosφ=cosαcosα2.
Do đó
A1H=a.sinφ=a√1−cos2αcos2α2
=acosα2√cos2α2−cos2α.
VABCD.A1B1C1D1=AB.AD.sinα.A1H=a2.sina.acosα2√cos2α2−cos2α=2a3sinα2√cos2α2−cos2α.

