Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Xét hai điểm M trên AD’ và N trên DB sao cho AM= DN= k (0< k <a\(\sqrt 2 \) ). Gọi P là trung điểm B’C’.
LG a
Tính cos của góc giữa hai đường thẳng AP và BC’.
Lời giải chi tiết:
Ta chọn hệ toạ độ Oxyz có gốc là đỉnh A, tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA' (h.105).
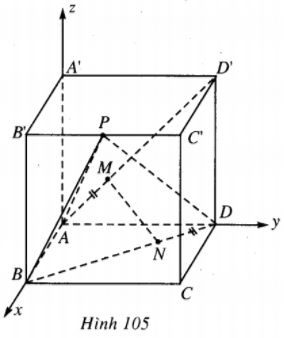
Khi đó :
\(\eqalign{ & A = \left( {0;0;0} \right) \cr & B = \left( {a;0;0} \right) \cr & D = \left( {0;a;0} \right) \cr & C = \left( {a;a;0} \right) \cr} \) \(\eqalign{ & A' = \left( {0;0;a} \right) \cr & B' = \left( {a;0;a} \right) \cr & D' = \left( {0;a;a} \right) \cr & C' = \left( {a;a;a} \right) \cr} \)
\(P = \left( {a;{a \over 2};a} \right)\)
Ta có \(\overrightarrow {AP} = \left( {a;{a \over 2};a} \right)\)
\(\overrightarrow {BC'} = \left( {0;a;a} \right).\)
Gọi \(\alpha \) là góc giữa hai đường thẳng \(AP\) và \(BC'\) ta có :
\(\cos \alpha = {{\left| {0 + {{{a^2}} \over 2} + {a^2}} \right|} \over {\sqrt {{a^2} + {{{a^2}} \over 2} + {a^2}} .\sqrt {{a^2} + {a^2}} }} = {1 \over {\sqrt 2 }} \Rightarrow \alpha = {45^o}\)
LG b
Tính thể tích khối tứ diện APBC’.
Lời giải chi tiết:
Ta có : \(\overrightarrow {AP} = \left( {a;{a \over 2};a} \right)\), \(\overrightarrow {AB} = {\rm{ }}\left( {a;0;0} \right),\overrightarrow {AC'} = (a;a;a)\)
\(\eqalign{ & \Rightarrow \left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right] = \left( {\left| {\matrix{ {{a \over 2}} & a \cr 0 & 0 \cr } } \right|;\left| {\matrix{ a & a \cr 0 & a \cr } } \right|;\left| {\matrix{ a & {{a \over 2}} \cr a & 0 \cr } } \right|} \right) \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \left( {0;{a^2}; - {{{a^2}} \over 2}} \right) \cr & \Rightarrow \left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right].\overrightarrow {AC'} = 0 + {a^3} - {{{a^3}} \over 2} = {{{a^3}} \over 2}. \cr} \)
Vậy \({V_{APBC'}} = {1 \over 6}\left| {\left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right].\overrightarrow {AC'} } \right| = {1 \over 6}.{{{a^3}} \over 2} = {{{a^3}} \over {12}}.\)
LG c
Chứng minh MN luôn song song với mặt phẳng (A’D’CB) khi k thay đổi.
Lời giải chi tiết:
Mặt phẳng \(\left( {A'D'CB} \right)\) song song với trục Oy nên có phương trình :
\(px{\rm{ }} + {\rm{ }}qz{\rm{ }} + {\rm{ }}n{\rm{ }} = 0\) \(\left( {n \ne 0,{p^2} + {q^2} > 0} \right).\)
Vì mặt phẳng này đi qua \(A',B,C\) nên ta xác định được p = q và n = -pa.
Cho p = 1, ta được phương trình mp\(\left( {A'D'CB} \right)\) là \(x + z - {\rm{ }}a = {\rm{ }}0\). Vectơ pháp tuyến của mặt phẳng này là \(\overrightarrow n = {\rm{ }}\left( {1{\rm{ }};{\rm{ }}0{\rm{ }};{\rm{ }}1} \right).\)
Từ giả thiết \(M \in AD',{\rm{ }}N \in DB;{\rm{ }}AM = {\rm{ }}DN = k\), ta tính được :
\(M = \left( {0;{k \over {\sqrt 2 }};{k \over {\sqrt 2 }}} \right),N = \left( {{k \over {\sqrt 2 }};{{a\sqrt {2 } -k} \over {\sqrt 2 }};0} \right).\)
Suy ra \(\overrightarrow {MN} = \left( {{k \over {\sqrt 2 }};{{a\sqrt {2 } -2k} \over {\sqrt 2 }}; - {k \over {\sqrt 2 }}} \right).\)
Ta có \(\overrightarrow {MN} .\overrightarrow n = 1.{k \over {\sqrt 2 }} + 0\left( {{{a\sqrt {2 }-2 k} \over {\sqrt 2 }}} \right) + 1.\left( { - {k \over {\sqrt 2 }}} \right) = 0\)
\(\Rightarrow \overrightarrow {MN} \bot \overrightarrow n .\)
Rõ ràng \(N \notin mp\left( {A'D'CB} \right).\) Suy ra MN song song với mp\(\left( {A'D'CB} \right).\)
LG d
Tìm k để đoạn MN ngắn nhất.
Lời giải chi tiết:
Ta có \(M{N^2} = {\left( {{k \over {\sqrt 2 }}} \right)^2} + {\left( {{{a\sqrt {2 }-2 k} \over {\sqrt 2 }}} \right)^2} + {\left( { - {k \over {\sqrt 2 }}} \right)^2}.\)
\(\eqalign{ & = 3{k^2} - 2a\sqrt 2 k + {a^2} \cr & = 3\left[ {{{\left( {k - {{a\sqrt 2 } \over 3}} \right)}^2} + {{{a^2}} \over 9}} \right] \ge 3{{{a^2}} \over 9} = {{{a^2}} \over 3}. \cr} \)
\(M{N^2}\) nhỏ nhất bằng \({{{a^2}} \over 3}\) khi \(k = {{a\sqrt 2 } \over 3}\) (thoả mãn điều kiện \(0{\rm{ }} < k{\rm{ }} < {\rm{ }}a\sqrt 2 \) ).
Vậy MN ngắn nhất bằng \({{a\sqrt 3 } \over 3}\) khi \(k = {{a\sqrt 2 } \over 3}\).
LG e
Khi đoạn MN ngắn nhất, chứng minh rằng MN là đường vuông góc chung của AD’ và DB, đồng thời MN song song với A’C.
Lời giải chi tiết:
Khi MN ngắn nhất thì \(k = {{a\sqrt 2 } \over 3}\) Khi đó \(\overrightarrow {MN} = \left( {{a \over 3};{a \over 3};{{ - a} \over 3}} \right).\)
Ta lại có \(\overrightarrow {AD'} = {\rm{ }}\left( {0;a;{\rm{ }}a} \right),\overrightarrow {DB} {\rm{ }} = (a; - a;0)\) nên \(\overrightarrow {MN} .\overrightarrow {AD'} = {\rm{ }}0,\overrightarrow {MN} .\overrightarrow {DB} = {\rm{ }}0.\)
Vậy MN là đường vuông góc chung của AD' và DB.
Mặt khác \(\overrightarrow {A'C} = \left( a;a; - a\right) = 3\overrightarrow {MN} \), chứng tỏ \(\overrightarrow {MN} \), \(\overrightarrow {A'C} \) cùng phương. Do \(N \not\in A'C\) nên \(MN//A'C.\)

