Đề bài
Hãy tính thể tích của khối hộp nếu biết độ dài cạnh bên bằng a, diện tích hai mặt chéo lần lượt là S1,S2 và góc giữa hai mặt chéo bằng α.
Lời giải chi tiết
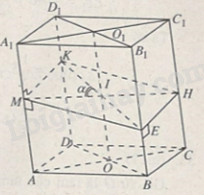
Giả sử hình hộp đã cho là ABCD.A1B1C1D1.
Gọi OO1 là giao tuyến của hai mặt chéo.
Trong hai mặt chéo (A1C1CA) và (B1D1DB), qua điểm I∈OO1, ta lần lượt kẻ hai đường thẳng KE và MH đều vuông góc với OO1.
Khi đó α=(MH,KE) và MEHK là thiết diện thẳng khối hộp.
Đặt KE=x,MH=y thì SMEHK=12xysinα.
Áp dụng kết quả bài tập 30, ta có:
Vhộp = SMKHE.AA1=12xyasinα.
Nhưng xa=S1,ya=S2 suy ra x=S1a,y=S2a
⇒xy=S1S2a2.
Vậy Vhộp=S1S2sinα2a.
Loigiaihay.com

