Câu 1.
Hình chóp D.ABC có \(DA \bot mp(ABC),\) đáy ABC là tam giác vuông tại B. Đặt AB = c, BC = a, AD = b. Bán kính mặt cầu ngoại tiếp hình chóp bằng
\(\eqalign{ & (A)\;{1 \over 3}\sqrt {{a^2} + {b^2} + {c^2}} ; \cr & (B)\;{1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} ; \cr & (C)\;\sqrt {{a^2} + {b^2} + {c^2}} ; \cr & (D)\;2\sqrt {{a^2} + {b^2} + {c^2}} . \cr} \)
Lời giải chi tiết:
Chọn (B).
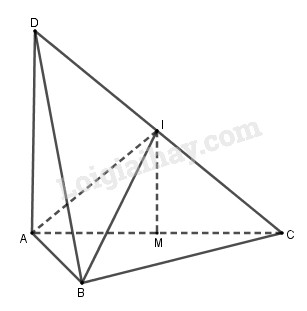
Ta có: \(\left\{ \begin{array}{l}CB \bot AB\\CB \bot DA\end{array} \right.\)\( \Rightarrow CB \bot \left( {DAB} \right) \Rightarrow CB \bot DB\)
Gọi \(I\) là trung điểm của \(CD\).
Dễ thấy các tam giác \(DAC,DBC,ABC\) vuông có cạnh huyền \(DC\) nên \(ID = IC = IA = IB\)
Do đó \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).
Ta có:
\(\begin{array}{l}IA = \frac{1}{2}DC = \frac{1}{2}\sqrt {D{A^2} + A{C^2}} \\ = \frac{1}{2}\sqrt {D{A^2} + A{B^2} + B{C^2}} \\ = \frac{1}{2}\sqrt {{a^2} + {b^2} + {c^2}} \end{array}\)
Câu 2.
Cho điểm A và đường thẳng d không đi qua A. Xét các mặt cầu có tâm thuộc d và đi qua điểm A. Trong các mệnh đề sau đây, mệnh đề nào đúng ?
(A) Các mặt cầu đó luôn đi qua một điểm cố định;
(B) Các mặt cầu đó luôn đi qua hai điểm cố định;
(C) Các mặt cầu đó luôn đi qua một đường tròn cố định;
(D) Cả ba mệnh đề trên đều sai.
Lời giải chi tiết:
Chọn (C ).
Câu 3.
Cho bốn điểm A, B, C,D cùng thuộc một mặt cầu và \(\widehat {ADB} = \widehat {BDC} = \widehat {CDA}\) =900. Một đường kính của mặt cầu đó là
(A) AB;
(B) BC;
(C ) AC;
(D) DD’, trong đó \(\overrightarrow {DD'} = 3\overrightarrow {DG} \) với G là trọng tâm tam giác ABC.
Lời giải chi tiết:
Chọn (D).

Tứ diện ABCD vuông tại D nên dựng hình hộp chữ nhật như trên ta thấy:
8 điểm A, B, C, D, E, F, D’, H cùng thuộc mặt cầu đã cho.
Đường kính mặt cầu này là DD’.
Ngoài ra \(\overrightarrow {DD'} = 3\overrightarrow {DG} \) (đã biết từ lớp 11) nên chọn D.
Câu 4.
Cho mặt cầu (S1) bán kính R1, mặt cầu (S2) có bán kính bằng R2 mà \({R_2} = 2{R_1}\). Tỉ số diện tích của mặt cầu (S2) và mặt cầu (S1) bằng
\(\eqalign{ & (A)\;{1 \over 2}; \cr & (B)\;2; \cr & (C)\;3; \cr & (D)\;4. \cr} \)
Lời giải chi tiết:
Chọn (D).
\(\frac{{{S_2}}}{{{S_2}}} = \frac{{4\pi R_2^2}}{{4\pi R_1^2}} = {\left( {\frac{{{R_2}}}{{{R_1}}}} \right)^2} = {\left( {\frac{{2{R_1}}}{{{R_1}}}} \right)^2} = 4\)
Câu 5.
Cho mặt phẳng (P) và điểm S nằm ngoài (P). Gọi A là điểm cố định thuộc (P) sao cho SA không vuông góc với (P). Một đường thẳng d thay đổi, nằm trong (P) và luôn đi qua A. Tập hợp các hình chiếu của điểm S trên đường thẳng d là
(A) Một mặt cầu;
(B) Một mặt trụ;
(C) Một mặt nón;
(D) Một đường tròn.
Lời giải chi tiết:
Chọn (D).
Câu 6.
Cho điểm A cố định thuộc mặt cầu (S). Ba đường thẳng thay đổi đi qua A, đôi một vuông góc và cắt mặt cầu (S) tại B, C, D. Xét hình hộp chữ nhật dựng trên ba cạnh AB, AC, AD. Trong các mệnh đề sau, mệnh đề nào đúng ?
(A)Hình hộp đó có một đường chéo cố định;
(B) Hình hộp đó có hai đường chéo cố định;
(C ) Hình hộp đó có ba đường chéo cố định;
(D) Hình hộp đó có không đường chéo cố định.
Lời giải chi tiết:
Chọn (A).
Câu 7.
Cho tam giác đều ABC cạnh a. Gọi (P) là mặt phẳng qua BC và vuông góc với mp(ABC). Trong mp(P), xét đường tròn (C ) đường kính BC. Bán kính của mặt cầu (S) đi qua (C ) và điểm A bằng
\(\eqalign{ & (A)\;a\sqrt 3 ; \cr & (B)\;{{a\sqrt 3 } \over 2}; \cr & (C)\;{{a\sqrt 3 } \over 3}; \cr & (D)\;{{a\sqrt 3 } \over 4}. \cr} \)
Lời giải chi tiết:
Chọn (C ).
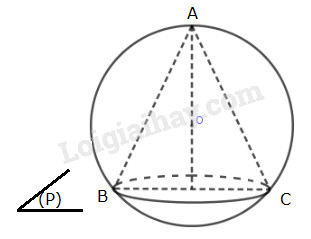
Tam giác ABC đều cạnh a nên đường cao \(h = \frac{{a\sqrt 3 }}{2}\).
Bán kính mặt cầu \(AO = \frac{2}{3}h = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
Câu 8.
Gọi \({O_1},{O_2},{O_3}\) lần lượt là tâm các mặt cầu ngoại tiếp, nội tiếp, tiếp xúc với các cạnh của một hình lập phương. Trong các mệnh đề sau, mệnh đề nào đúng ?
(A) O1 trùng với O2;
(B) O2 trùng với O3;
(C ) O3 trùng với O1;
(D) O1, O2, O3 trùng nhau.
Lời giải chi tiết:
Chọn (D).
Câu 9.
Kí hiệu R1, R2, R3 lần lượt là bán kính của các mặt cầu ngoại tiếp, nội tiếp, tiếp xúc với các cạnh của một hình lập phương. Khi ấy :
\(\eqalign{ & (A)\;{R_1} > {R_2} > {R_3}; \cr & (B)\;{R_2} > {R_3} > {R_1}; \cr & (C)\;{R_1} > {R_3} > {R_2}; \cr & (D)\;{R_3} > {R_1} > {R_2}. \cr} \)
Lời giải chi tiết:
Chọn (C ).
Câu 10.
Cho hình chóp tứ giác đều S.ABCD có các cạnh cùng bằng a. Bán kính mặt cầu ngoại tiếp hình chóp đó là
\(\eqalign{ & (A)\;a\sqrt 2 ; \cr & (B)\;{{a\sqrt 2 } \over 2}; \cr & (C)\;a\sqrt 3 ; \cr & (D)\;{{a\sqrt 3 } \over 2}. \cr} \)
Lời giải chi tiết:
Chọn (B ).
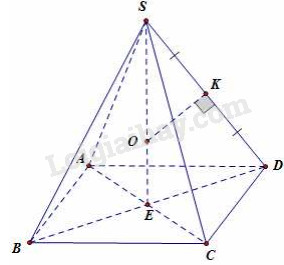
Mặt cầu cần tìm tâm \(O\) (hình vẽ)
Ta có:
\(\begin{array}{l}\Delta SOK \sim \Delta SDE \Rightarrow \frac{{SO}}{{SD}} = \frac{{SK}}{{SE}}\\ \Rightarrow SO = \frac{{SD.SK}}{{SE}} = \frac{{SD.SK}}{{\sqrt {S{D^2} - D{E^2}} }}\\ = \frac{{a.\frac{a}{2}}}{{\sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} }} = \frac{{a\sqrt 2 }}{2}\end{array}\)
Câu 11.
Cho hình chóp tứ giác đều S.ABCD có các cạnh cùng bằng a. Bán kính mặt cầu nội tiếp hình chóp đó là
\(\eqalign{ & (A)\;{{a\sqrt 2 } \over {2(1 + \sqrt 3 )}}; \cr & (B)\;{{a\sqrt 2 } \over {4(1 + \sqrt 3 )}}; \cr & (C)\;{{a\sqrt 3 } \over {2(1 + \sqrt 3 )}}; \cr & (D)\;{{a\sqrt 3 } \over {4(1 + \sqrt 3 )}}. \cr} \)
Lời giải chi tiết:
Chọn (A ).

Gọi I và \(r\) là tâm, bán kính mặt cầu nội tiếp hình chóp, ta có:
\(\begin{array}{l}{V_{S.ABCD}}\\ = {V_{I.SAB}} + {V_{I.SBC}} + {V_{I.SCD}}\\\,\,\,\, + {V_{I.SDA}} + {V_{I.ABCD}}\\ = \frac{1}{3}r.{S_{SAB}} + \frac{1}{3}r.{S_{SBC}} + \frac{1}{3}r.{S_{SCD}}\\\,\,\,\, + \frac{1}{3}r.{S_{SDA}} + \frac{1}{3}r.{S_{ABCD}}\\ = \frac{1}{3}r{S_{tp}}\\ \Rightarrow r = \frac{{3{V_{S.ABCD}}}}{{{S_{tp}}}}\end{array}\)
Gọi O là tâm hình vuông ABCD ta có:
\(\begin{array}{l}SO = \sqrt {S{D^2} - D{O^2}} \\ = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\end{array}\)
Thể tích khối chóp \(S.ABCD\) là:
\({V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}}\) \( = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\)
\(\begin{array}{l}{S_{tp}} = 4{S_{ABC}} + {S_{ABCD}}\\\,\,\,\,\,\,\, = 4.\frac{{{a^2}\sqrt 3 }}{4} + {a^2}\\\,\,\,\,\,\,\, = {a^2}\left( {1 + \sqrt 3 } \right)\end{array}\)
Vậy \(r = \frac{{3{V_{S.ABCD}}}}{{{S_{tp}}}}\) \( = \frac{{3.\frac{{{a^3}\sqrt 2 }}{6}}}{{{a^2}\left( {1 + \sqrt 3 } \right)}} = \frac{{a\sqrt 2 }}{{2\left( {1 + \sqrt 3 } \right)}}\)
Câu 12.
Cho hình lăng trụ tam giác đều có các cạnh cùng bằng a. Diện tích mặt cầu ngoại tiếp hình lăng trụ là
\(\eqalign{ & (A)\;7\pi {a^2}; \cr & (B)\;{{7\pi {a^2}} \over 2}; \cr & (C)\;{{7\pi {a^2}} \over 3}; \cr & (D)\;{{7\pi {a^2}} \over 6}. \cr} \)
Lời giải chi tiết:
Chọn (C ).

Gọi O, O’ lần lượt là tâm hai tam giác đáy \(ABC\) và \(A'B'C'\).
Khi đó trung điểm \(I\) của \(OO'\) là tâm mặt cầu cần tìm.
Bán kính
\(\begin{array}{l}AI = \sqrt {A{O^2} + O{I^2}} \\ = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {21} }}{6}\end{array}\)
Diện tích mặt cầu:
\(S = 4\pi A{I^2}\) \( = 4\pi .{\left( {\frac{{a\sqrt {21} }}{6}} \right)^2} = \frac{{7\pi {a^2}}}{3}\)
Câu 13.
Cho tam giác đều ABC cạnh a. Gọi (P) là mặt phẳng qua BC và vuông góc với mp(ABC). Trong (P), xét đường tròn (C ) đường kính BC. Diện tích mặt cầu nội tiếp hình nón có đáy là (C ), đỉnh là A bằng
\(\eqalign{ & (A)\;{{\pi {a^2}} \over 2}; \cr & (B)\;{{\pi {a^2}} \over 3}; \cr & (C)\;\pi {a^2}; \cr & (D)\;2\pi {a^2}. \cr} \)
Lời giải chi tiết:
Chọn (B).

Bán kính mặt cầu nội tiếp hình nón là:
\(IH = \frac{1}{3}AH\) \( = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\)
Diện tích mặt cầu:
\(S = 4\pi I{H^2}\) \( = 4\pi .{\left( {\frac{{a\sqrt 3 }}{6}} \right)^2} = \frac{{\pi {a^2}}}{3}\)
Câu 14.
Cho hai điểm A, B cố định. M là điểm di động trong không gian sao cho \(\widehat {MAB}\) = 300. Trong các mệnh đề sau, mệnh đề nào đúng ?
(A) M thuộc mặt cầu cố định;
(B) M thuộc mặt trụ cố định;
(C) M thuộc mặt phẳng cố định;
(D) M thuộc mặt nón cố định;
Lời giải chi tiết:
Chọn (D).
Câu 15.
Cho hai đường thẳng song song a và b. Gọi (P) và (Q) là các mặt phẳng thay đổi lần lượt đi qua a, b và vuông góc với nhau. Gọi c là giao tuyến của (P) và (Q). Trong các mệnh đề sau, mệnh đề nào đúng ?
(A) c thuộc mặt phẳng cố định;
(B) c thuộc mặt trụ cố định;
(C) c thuộc mặt nón cố định;
(D) Cả ba mệnh đề trên đều sai.
Lời giải chi tiết:
Chọn (B).

