Cho đường tròn đường kính AB = 2R nằm trong mặt phẳng (P) và một điểm M nằm trên đường tròn đó sao cho ^MAB=α. Trên đường thẳng vuông góc với (P) tại A, lấy điểm S sao cho SA=h. Gọi H và K lần lượt là hình chiếu vuông góc của A trên SM và SB.
LG a
Chứng minh rằng SB⊥mp(KHA).
Lời giải chi tiết:
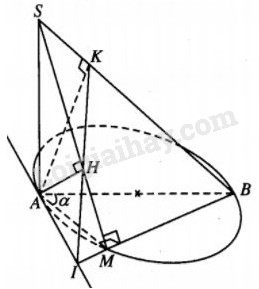
Ta có BM⊥AM (vì M nằm trên đường tròn đường kính AB) và BM⊥SA (do SA⊥(P)), suy ra BM⊥(SAM)⇒BM⊥AH.
Mặt khác AH⊥SM, suy ra AH⊥SB,
Theo giả thiết , ta lại có AK⊥SB
Vậy SB⊥(KHA).
LG b
Gọi I là giao điểm của HK với (P). Hãy chứng minh AI là tiếp tuyến của đường tròn đã cho.
Lời giải chi tiết:
Vì SB⊥(KHA) nên SB⊥AI, mặt khác SA⊥AI nên AI⊥AB, mà AI thuộc mp(P), suy ra AI là tiếp tuyến của đường tròn đã cho tại điểm A.
LG c
Cho h = 2R, α=300, tính thể tích khối chóp S.KHA.
Lời giải chi tiết:
Cách 1. Ta có :
VS.KHAVS.BMA=SKSB.SHSM=SK.SBSB2.SH.SMSM2=SA4SB2.SM2=(2R)4(4R2+4R2).(4R2+AM2)=2R24R2+4R2.cos2α=12(1+cos2α),VS.BMA=13SBMA.SA=16AM.BM.SA=162Rcosα.2Rsinα.2R=2R33sin2α=2R33.√32=R3√32.
Vậy VS.KHA=12(1+cos2α).R3√33
=12(1+34).R3√33=2R3√321
Cách 2. Dễ thấy VS.KHA=13SKHA.SK.
Dùng hệ thức lượng trong tam giác vuông, ta có thể tính được SK, AH, AK, HK ( với chú ý rằng tam giác KHA vuông ở H) theo R. Từ đó tính được thể tích khối chóp S.KHA.

