Đề bài
Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt khối lập phương ). Biết cạnh của khối lập phương bằng a, hãy tính thể tích của khối tám mặt đều đó.
Lời giải chi tiết
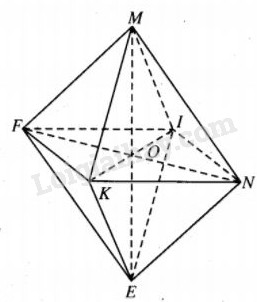
Gọi độ dài của khối bát diện đều là b . Khối bát diện đều có thể phân chia thành hai khối chóp tứ giác đều mà các cạnh bằng b ; M.FKNI và E.FKNI.
Gọi MO là đường cao của khối chóp M.FKNI thì ON bằng một nửa đường chéo của đáy.
Ta có
\(\eqalign{ & M{O^2} = M{N^2} - O{N^2} = {b^2} - {\left( {b{{\sqrt 2 } \over 2}} \right)^2} = {{{b^2}} \over 2} \cr & \Rightarrow MO = b{{\sqrt 2 } \over 2}. \cr & {V_{M.FKNI}} = {1 \over 3}{S_{FKNI}}.MO = {1 \over 3}{b^2}.b{{\sqrt 2 } \over 2} = {{{b^3}\sqrt 2 } \over 6}. \cr} \)
Như ta đã biết, b bằng một nửa đường chéo của một mặt của khối lập phương ngoại tiếp.
Do đó \(b = {{a\sqrt 2 } \over 2}\)và \({V_{M.FKNI}} = {\left( {{{a\sqrt 2 } \over 2}} \right)^3}.{{\sqrt 2 } \over 6} = {{{a^3}} \over {12}}.\)
Vậy thể tích khối bát diện đều là :
\(V = 2{V_{M.FKNI}} = {{{a^3}} \over 6}.\)
