LG a
Tìm cực đại các hệ số m, n, p sao cho hàm số
\(f(x) = - {1 \over 3}{x^3} + m{x^2} + nx + p\)
Đạt cực đại tại điểm x = 3 và đồ thị (C) của nó tiếp xúc với đường thẳng \(y = 3x - {1 \over 3}\) tại giao điểm của (C) với trục tung
Lời giải chi tiết:
Đường thẳng \(y = 3x - {1 \over 3}\) cắt trục tung tại điểm \(A\left( {0; - {1 \over 3}} \right)\)
Vì đồ thị (C) của hàm số đã cho đi qua điểm A nên \(f(0) = p = - {1 \over 3}\)
Ta có \(f'(x) = - {x^2} + 2mx + n\).
Vì (C) tiếp xúc với đường thẳng \(y = 3x - {1 \over 3}\) tại điểm A nên \(f'(0) = n = 3\)
Do hàm số đạt cực đại tại điểm x = 3 nên \(f'(3) = - 9 + 6m + 3 = 0\)
\(\Leftrightarrow m = 1\).
Với các giá trị m, n, p vừa tìm được, ta có hàm số
\(f(x) = - {1 \over 3}{x^3} + {x^2} + 3x + {1 \over 3}\)
Khi đó, \(f''(x) = - 2x + 2\) và \(f''(3) = - 4 < 0\).
Hàm số đạt cực đại tại điểm x = 3.
LG b
Khảo sát sự biến thiên và vẽ đồ thị của hàm số với các giá trị vừa tìm được của m, n, p
Lời giải chi tiết:
+) TXĐ: \(D = \mathbb{R}\).
+) Chiều biến thiên:
\(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ,\mathop {\lim }\limits_{x \to - \infty } y = + \infty \)
\(\begin{array}{l}y' = - {x^2} + 2x + 3\\y' = 0 \Leftrightarrow - {x^2} + 2x + 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right.\end{array}\)
BBT:
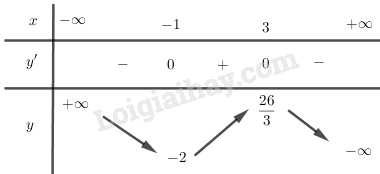
Hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {3; + \infty } \right)\).
Hàm số đồng biến trên \(\left( { - 1;3} \right)\).
Hàm số đạt cực đại tại \(x = 3,{y_{CD}} = \frac{{26}}{3}\)
Hàm số đạt cực tiểu tại \(x = - 1,{y_{CT}} = - 2\).
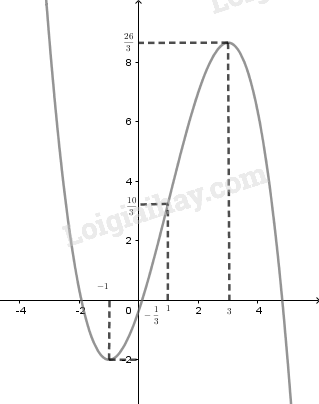
+) Đồ thị:
\(\begin{array}{l}y'' = - 2x + 2\\y'' = 0 \Leftrightarrow - 2x + 2 = 0\\ \Leftrightarrow x = 1 \Rightarrow y\left( 1 \right) = \frac{{10}}{3}\end{array}\)
Điểm uốn \(I\left( {1;\frac{{10}}{3}} \right)\).
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0; - \frac{1}{3}} \right)\).
Điểm cực đại \(\left( {3;\frac{{26}}{3}} \right)\) và điểm cực tiểu \(\left( { - 1; - 2} \right)\).