Cho hình chóp S.ABC. Biết rằng có một mặt cầu bán kính r tiếp xúc với các cạnh của hình chóp và tâm I của mặt cầu nằm trên đường cao SH của hình chóp.
LG a
Chứng minh rằng S.ABC là hình chóp đều.
Lời giải chi tiết:
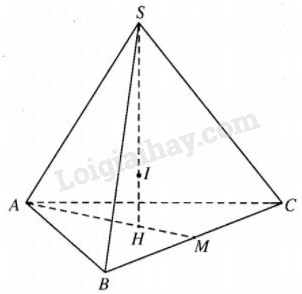
Vì các cạnh của hình chóp tiếp xúc với mặt cầu nên
SA+BC = SB+AC = SC+AB
Mặt khác , tâm I của mặt cầu thuộc đường cao SH nên dễ thấy \(\widehat {ISA} = \widehat {ISB} = \widehat {ISC},\) tức là \(\widehat {HSB} = \widehat {HSA} = \widehat {HSC},\) từ đó SA=SB=SC.
Vậy AB = BC = CA, từ đó S.ABC là hình chóp đều.
LG b
Tính đường cao của hình chóp biết rằng \({\rm{IS = r}}\sqrt 3 .\)
Lời giải chi tiết:
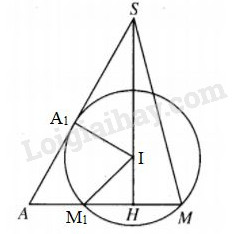
Đặt SH = h.
Gọi M là trung điểm của BC thì mp(SAM) cắt mặt cầu theo đường tròn lớn, đường tròn này tiếp xúc với SA tại A1, đi qua điểm M và cắt AM tại M1, dễ thấy AM1 = M1H = HM.
Vì \(\Delta S{A_1}I \sim \Delta SHA\) nên \({{{A_1}I} \over {SI}} = {{AH} \over {SA}},\)
Từ đó \({r \over {r\sqrt 3 }} = {{AH} \over {\sqrt {{h^2} + A{H^2}} }}.\)
Từ AH = 2M1H suy ra
\(\eqalign{ & A{H^2} = 4{M_1}{H^2} = 4(IM_1^2 - I{H^2}). \cr & = 4\left[ {{r^2} - {{(h - r\sqrt 3 )}^2}} \right]. \cr} \)
Vậy
\(\eqalign{ & {1 \over {\sqrt 3 }} = {{2\sqrt {{r^2} - {{(h - r\sqrt 3 )}^2}} } \over {\sqrt {{h^2} + 4\left[ {{r^2} - {{(h - r\sqrt 3 )}^2}} \right]} }} \cr & \Leftrightarrow 9{h^2} - 16rh\sqrt 3 + 16{r^2} = 0 \cr & \Leftrightarrow h = {{4r} \over {\sqrt 3 }}(do\;\,h > {\rm{IS > r)}}{\rm{.}} \cr} \)

