Cho hai đường thẳng chéo nhau d1, d2 nhận IJ là đường vuông góc chung (I∈d1,J∈d2),IJ=a. Gọi (P) là mặt phẳng đi qua điểm I và vuông góc với d2, đặt α là góc giữa d1 và (P). Xét một mặt phẳng (Q) song song với (P) cắt d1, d2 lần lượt tại A1, A2. Gọi H1 là hình chiếu của A1 trên (P).
LG1
Chứng minh rằng các điểm I, J, A1, A2, H1 cùng thuộc một mặt cầu. Chỉ rõ tâm của mặt cầu đó và tính diện tích mặt cầu theo a, α và khoảng cách h giữa hai mặt phẳng (P), (Q)
Lời giải chi tiết:
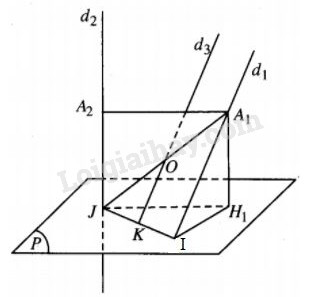
Vì (P) đi qua I và (P)⊥d2,IJ⊥d2 nên IJ⊂(P).
Vì H1 là hình chiếu của A1 trên (P) nên ^A1IH1=α và A1H1//d2. Do mp(Q) song song với mp(P) và (Q) cắt d1, d2 tại A1, A2 nên A1A2//JH1.
Suy ra JH1A1A2 là hình chữ nhật.
Mặt khác ^JIA1=900 vậy các điểm I, J, A1, A2, H1 cùng thuộc một mặt cầu, tâm mặt cầu là trung điểm O của JA1, bán kính của mặt cầu là R=12JA1.
Ta có JA12=IJ2+IA21=a2+h2sin2α
Từ đó R=12sinα√a2sin2α+h2.
Diện tích mặt cầu là S=πsin2α(a2sin2α+h2).
LG 2
Chứng minh rằng khi mp(Q) thay đổi thì tâm mặt cầu nói trên luôn thuộc một đường thẳng cố định và mặt cầu ấy luôn đi qua một đường tròn cố định.
Lời giải chi tiết:
Khi mặt phẳng (Q) thay đổi thì A1 luôn thuộc d1 mà →JO=12→JA1, vậy O thuộc đường thẳng d3 đi qua trung điểm K của IJ và d3 song song với d1.
Xét mặt phẳng (R) chứa IJ và vuông góc với d3 thì (R ) cắt mặt cầu nêu trên theo đường tròn tâm K, mà K là trung điểm của IJ nên IJ là đường kính của đường tròn.
Đường tròn này cố định, từ đó ta có mặt cầu đi qua các điểm I, J, A1, A2, H1 luôn đi qua một đường tròn cố định.

