Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng đáy. Một mặt phẳng đi qua CD cất các cạnh SA, SB lần lượt tại M, N. Đặt AM = x.
LG a
Tứ giác MNCD là hình gì ? Tính diện tích tứ giác MNCD theo a, x.
Lời giải chi tiết:
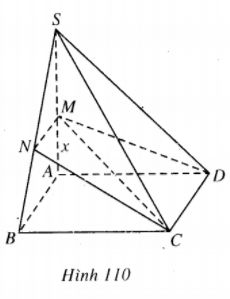
Do AB//CD,AB⊂(SAB),CD⊂(MNCD) nên hai mặt phẳng (SAB) và (MNCD) cắt nhau theo giao tuyến MN song song với AB và CD.
Mặt khác CD⊥(SAD)⇒CD⊥DM.
Vậy MNCD là hình thang vuông.
Vì MN//AB nên ta có MNAB=SMSA.
Vây MN=AB.SMSA=aSMa=SM=a−x.
SMNCD=12(MN+CD).DM
=12(a−x+a)√a2+x2=12(2a−x)√a2+x2.
LG b
Xác định giá trị của x để thể tích của hình chóp S.MNCD bằng 29 lần thể tích hình chóp S.ABCD.
Lời giải chi tiết:
SABCD=13SABCD.SA=13a3
=>VS.ACD=VS.ACB=16a3.
VS.MNCD=VS.MNC+VS.MCD.
Mặt khác
VS.MCNVS.ACB=SMSA.SCSC.SNSB=(a−xa)2
⇒VS.MCNVS.ABCD=12(a−xa)2.
VS.MCDVS.ACD=SMSA.SCSC.SDSD=SMSA=a−xa
⇒VS.MCDVS.ABCD=a−x2a.
VS.MNCDVS.ABCD=VS.MCN+VS.MCDVS.ABCD=VS.MCNVS.ABCD+VS.MCDVS.ABCD
=12(a−xa)2+a−x2a.
Từ đó ta có VS.MNCDVS.ABCD=29⇔9x2−27ax+14a2=0
⇔[x=73a ( loại vì theo giả thiết x < a)x=23a

