LG a
Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số
y=x+4x+2
Lời giải chi tiết:
+) TXĐ: D=R∖{−2}
+) Chiều biến thiên:
limx→±∞y=1 nên TCN y=1
limx→(−2)+y=+∞,limx→(−2)−y=−∞ nên TCĐ x=−2
Ta có:
y′=−2(x+2)2<0,∀x∈D
Hàm số nghịch biến trên các khoảng (−∞;−2) và (−2;+∞) nên không có cực trị.
BBT:
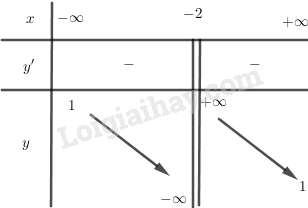
+) Đồ thị:
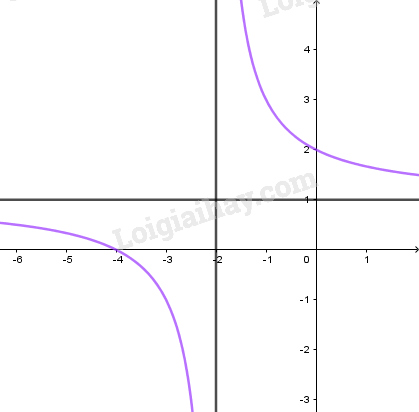
LG b
Chứng minh rằng parabol (P) có phương trình y=x2+2 tiếp xúc với đường cong (H). Xác đinh tiếp điểm và viết phương trình tiếp tuyến chung của (H) và (C) tại điểm đó.
Lời giải chi tiết:
Ta có:
f(x)=x+4x+2⇒f′(x)=−2(x+2)2g(x)=x2+2⇒g′(x)=2x
Hoành độ tiếp điểm là nghiệm của hệ:
{x+4x+2=x2+2(1)−2(x+2)2=2x(2)
(1)⇔x+4=(x2+2)(x+2)⇔x+4=x3+2x2+2x+4⇔x3+2x2+x=0⇔x(x+1)2=0⇔[x=0x=−1
Thay x=0 vào (2) không thỏa mãn.
Thay x=−1 vào (2) thỏa mãn phương trình nên hệ có nghiệm duy nhất x=−1.
Do đó (P) tiếp xúc (C ) tại điểm A(−1;3).
Có f′(−1)=g′(−1)=−2 nên phương trình tiếp tuyến:
y=−2(x+1)+3 hay y=−2x+1.
LG c
Xét vị trí tương đối của (P) và (H) (tức là xác định mỗi khoảng trên đó (P) nằm phía trên hay phía dưới (H).
Lời giải chi tiết:
Ta thấy:
x+4x+2≥x2+2⇔x2+2≤x+4x+2⇔x3+2x2+xx+2≤0⇔x(x+1)2x+2≤0⇔−2<x≤0
Do đó
+) Trên mỗi khoảng (−∞;−2) và (0;+∞), (P) nằm phía trên (H)
+) Trên khoảng (−2;0), (P) nằm phía dưới (H).
Loigiahay.com

