Đề bài
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h. Gọi I là trung điểm của cạnh bên SC. Tính khoảng cách từ điểm S đến mặt phẳng (ABI).
Lời giải chi tiết
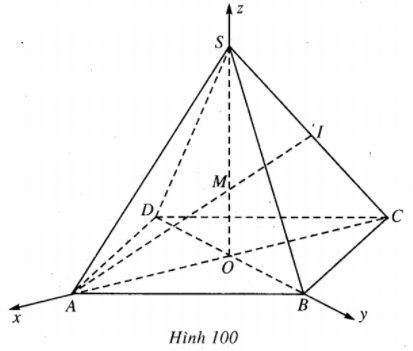
Ta chọn hệ trục Oxyz sao cho gốc tọa độ là tâm O của đáy, tia Ox chứa OA, tia Oy chứa OB, tia Oz chứa OS.
Khi đó :
A=(a√22;0;0),B=(0;a√22;0)C=(−a√22;0;0),S=(0;0;h)
Rõ ràng giao điểm M của SO và AI chính là trọng tâm tam giác SAC nên
M(0;0;h3)
Mặt phẳng (ABI) cũng chính là mặt phẳng (ABM). Vậy mp(ABI) có phương trình là :
xa√22+ya√22+zh3=1.
Do đó, khoảng cách từ S tới mặt phẳng (ABI) là :
d=|hh3−1|√(1a√22)2+(1a√22)2+(1h3)2=2√2a2+2a2+9h2
⇒d=2ah√4h2+9a2.

