Đề bài
Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O dến AB bằng a và ^SAO = 300, ^SAB = 600. Tính diện tích xung quanh hình nón.
Lời giải chi tiết
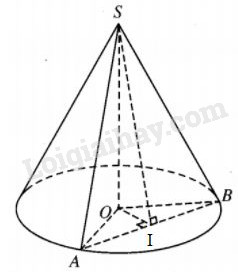
Gọi I là trung điểm của AB thì OI⊥AB,SI⊥AB,OI=a. Ta có
AO=SAcos ^SAO=√32SA.
AI=SAcos ^SAI=12SA.
Từ đó AIAO=1√3. Mặt khác AIAO=cos^IAO
⇒sin^IAO=√63=aOA.
Vậy OA=3a√6=a√62.
Xét tam giác SAO, ta có SA=OAcos300=a√62.2√3=a√2.
Từ đó diện tích xung quanh của hình nón đã cho là
Sxq=π.OA.SA=π.a√62.a√2=πa2√3.

