Một hình chóp với tứ giác đều ngoại tiếp hình cầu bán kính a
LG a
Chứng minh rằng thể tích của hình chóp là
V=4a2x23(x−2a).
Trong đó x là chiều cao của hình chóp.
Phương pháp giải:
Mặt phẳng đi qua đường cao SH của hình chóp và trung điểm M của một cạnh đáy cắt hình chóp theo tam giác cân SMN và cắt hình cầu theo tâm O bán kính a nội tiếp tam giác SMN.
Có thể tính thể tích hình chóp theo x và α=^SNH.
Sau đó sử dụng đẳng thức x=a+OS để tìm hệ thức giữa a, x và α.
Lời giải chi tiết:
Mặt phẳng đi qua đường cao SH của hình chóp và trung điểm M của một cạnh đáy cắt hình chóp theo tam giác cân SMN và cắt hình cầu theo tâm O bán kính a nội tiếp tam giác SMN.
Ta có HN=xcotα;MN=2xcotα.
Thể tích hình chóp là V=13MN2.SH=43x3cot2α
Ta tính cot2α theo a và x.
Từ đẳng thức SH = OH + OS ta có x=a+acosα; do đó cosα=ax−a
sin2α=1−cos2α
=1−a2(x−a)2=x2−2ax(x−a)2
cot2α=cos2αsin2α=a2x(x−2a)2
Từ đó suy ra công thức cần chứng minh.
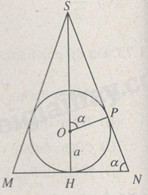
LG b
Với giá trị nào của x,hình chóp có thể tích là nhỏ nhất ?
Lời giải chi tiết:
Ta có:
V(x)=4a2x23(x−2a)V′(x)=43.2a2x(x−2a)−a2x2(x−2a)2=43.a2x2−4a3x(x−2a)2V′(x)=0⇔a2x2−4a3x=0⇔a2x(x−4a)=0⇔x=4a(dox>2a)
Lập BBT suy ra hàm số V(x) đạt GTNN tại x=4a.

