Lựa chọn câu để xem lời giải nhanh hơn
Cho hàm số f(x)=4πx−tanx,x∈[0;π4]
LG a
Xét chiều biến thiên của hàm số trên đoạn [0;π4]
Lời giải chi tiết:
Hàm số f liên tục tên nửa khoảng [0;π4] và có đạo hàm
f′(x)=4π−1cos2x=4−ππ−tan2x,x∈(0;π4)
f′(x)=0⇔tanx=√4−ππ
Dễ dàng thấy rằng 0<√4−ππ<1=tanπ4.
Do đó tồn tại một số duy nhất α∈(0;π4) sao cho tanα=√4−ππ
Bảng biến thiên
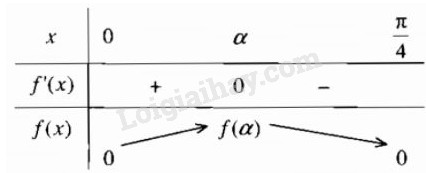
Hàm số đồng biến trên đoạn [0;α] và nghịch biến trên [α;π4]
LG b
Từ đó suy ra rằng: tanx≤4πx với mọi x∈[0;π4]
Lời giải chi tiết:
Theo bảng biến thiên ta có
f(x)≥0 với mọi x∈[0;π4]
Từ đó có bất đẳng thức cần chứng minh.

